MATHS-LYCEE.FR exercice corrigé chapitre Suites

En mode visiteur, vous ne disposez pas des fonctionnalités du site (documents vus, à revoir, validés, conseillés...)

92 documents pour le chapitre 3 Suites

Rappel: conseillé en fonction du niveau paramétré sur votre compte

Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.
*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)

niveau	Titre	infos	contenu
	COURS
	Suites parties 1 et 2	\| \| \|	- définition - relation de récurrence et forme explicites - étude des variations d'une suite
	Cours partie 3 suites arithmétiques	\| \| \|	- définition et forme explicite d'une suite arithmétique - exemples de base: déterminer si une suite est ou n'est pas arithmétique, recherche du premier terme et de la raison - somme des $n$ premiers entiers naturels - somme des termes consécutifs d'une suite arithmétique
	Cours partie 4 suites géométriques	\| \|	- définition et forme explicite - exemples de base somme des termes d'une suite géométrique
	Notion de limite (part 5)	\| \|	- approche de la limite avec un exemple notion de limite d'une suite - limite de $q^n$ et d'une suite géométrique
	AIDE MÉMOIRE
niveau	Titre	infos	contenu
conseillé	L'essentiel sur les suites	\| \|	- définition - - forme explicite et relation de récurrence - suites arithmétiques - suites géométriques - notion de limite
	MÉTHODES
niveau	Titre	infos	contenu
	réf 667-Étude des variations d'une suite	\| \|	- méthodes possibles - exemples types
	réf 747-Suites arithmétiques et géométriques	\| \|	- justifier qu'une suite est arithmétique - calculer la raison d'une suite arithmétique - somme des termes d'une suite arithmétique - justifier qu'une suite est géométrique - calculer la raison d'une suite géométrique - somme des termes d'une suite géométrique
	réf 1600-Suites arithmético-géométrique	\| \|	- justifier qu'une suite auxiliaire est géométrique - déterminer la forme explicite -étude des variations
	QCM
	réf 745-Suites et variations	\| \|	- calculs des termes d'une suite - utilisation des indices - étude des variations
	réf 746-Suites arithmétiques et géométriques	\| \|	Calcul des termes d\'une suite arithmétique Recherche de la raison connaissant deux termes de la suite arithmétique Calcul des termes d\'une suite géométrique Recherche de la raison connaissant deux termes de la suite suite géométrique Somme des termes consécutifs d'une suite arithmétique ou géométrique
	VIDÉOS
niveau	Titre	infos	contenu
	réf 668-Reconnaître une forme explicite ou une récurrence	\| \|	- déterminer si une suite est définie sous forme explicite ou par une relation de récurrence - calculs des premiers termes - utilisation de la calculatrice (CASIO)
	réf 670-Reconnaître une forme explicite ou une récurrence	\| \|	- déterminer si une suite est définie par une forme explicite ou une relation de récurrence - calcul des premiers termes - utilisation de la calculatrice (CASIO)
	réf 752-Calculs des termes d'une suite avec CASIO graphique	\| \|	- Suites avec CASIO graphique - calculs des termes d'une suite définie sous forme explicite - calcul des termes d'une suite définie par récurrence
	réf 753-Calculs des termes d'une suite avec calculatrice TI	\| \|	- Suites avec calculatrice TI et TI premium - calculs des termes d'une suite définie sous forme explicite - calcul des termes d'une suite définie par récurrence
	réf 751-Détermination graphique des termes avec une suite par récurrence	\| \|	- placer les termes d'une suite en utilisant le graphique de la fonction associée
	réf 669-Étude des variations avec $u_{n+1}-u_n$	\| \|	- étude des variations avec le signe de la différence de deux termes consécutifs
	réf 671-Étude des variations avec la fonction associée	\| \|	- fonction associée à une suite sous forme explicite - étude des variations d'une fonction avec sa dérivée
	réf 737-Justifier qu'une suite est arithmétique	\| \|	- méthode et exemple pour justifier qu'une suite est arithmétique
	réf 738-Déterminer la raison d'une suite arithmétique	\| \|	- calculer la raison d'une suite arithmétique connaissant deux termes - relation entre deux termes d'une suite arithmétique
	réf 739-Somme des termes d'une suite arithmétique	\| \|	- rappel du cours - exemple de calcul de la somme des termes d'une suite arithmétique
	réf 740-Justifier qu'une suite est géométrique	\| \|	- rappel de cours - justifier qu'une suite est géométrique et donner sa raison
	réf 741-Déterminer la raison d'une suite géométrique	\| \|	- rappel de cours - calculer la raison d'une suite géométrique
	réf 742-Somme des termes d'une suite géométrique	\| \|	- rappel du cours - calculer la somme des termes d'une suite géométrique
	EXERCICES
série 1	Démonstrations de cours
niveau	Titre	infos	contenu
	réf 748-Somme des entiers naturels aperçu exercice nº 748 Somme des entiers naturels Ouvrir l'exercice	\| \|	- étude d'un exemple - expression de la somme $S=1+2+3+...+n$
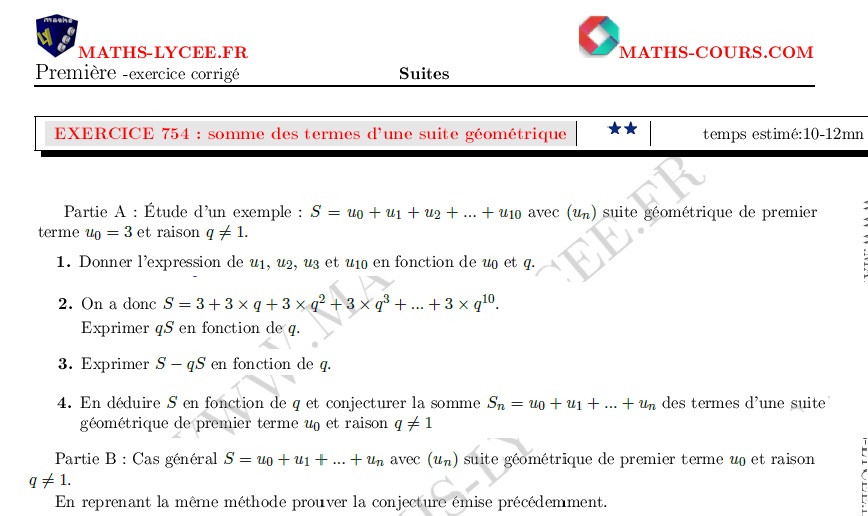
	réf 754-Somme des termes d'une suite géométrique aperçu exercice nº 754 Somme des termes d'une suite géométrique Ouvrir l'exercice	\| \|	- étude d'un exemple - démonstration du cas général
série 2	Calculs des termes
niveau	Titre	infos	contenu
	réf 674-Calcul des termes avec une forme explicite aperçu exercice nº 674 Calcul des termes avec une forme explicite Ouvrir l'exercice	\| \| \|	- calcul des premiers termes d'une suite - suite définie sous forme explicite
	réf 675-Reconnaître une forme explicite ou une récurrence aperçu exercice nº 675 Reconnaître une forme explicite ou une récurrence Ouvrir l'exercice	\| \| \|	- déterminer si une suite est définie par récurrence ou sous forme explicite - fonction associée - calcul des termes
	réf 676-Suite définie par récurrence aperçu exercice nº 676 Suite définie par récurrence Ouvrir l'exercice	\| \| \|	- calcul des termes avec une relation de récurrence - reconnaître une récurrence
	réf 678-Suite définie par récurrence aperçu exercice nº 678 Suite définie par récurrence Ouvrir l'exercice	\| \|	- reconnaître une relation de récurrence - calcul des premiers termes
	réf 677-Travail avec les indices (forme explicite) aperçu exercice nº 677 Travail avec les indices (forme explicite) Ouvrir l'exercice	\| \| \|	- suite définie sous forme explicite - expression de $u_{?n-1}$ et de $u_{n+1}$
	réf 679-Suites liées aperçu exercice nº 679 Suites liées Ouvrir l'exercice	\| \| \|	- suites liées par une relation de récurrence - calcul des termes
	réf 680-Calculs sur les indices-suites liées aperçu exercice nº 680 Calculs sur les indices-suites liées Ouvrir l'exercice	\| \|	- suite définie sous forme explicite - suites liées - recherche de la forme explicite
	réf 681-Détermination graphique avec une forme explicite aperçu exercice nº 681 Détermination graphique avec une forme explicite Ouvrir l'exercice	\| \| \|	- suite définie sous forme explicite et fonction associée - fonction affine - parabole
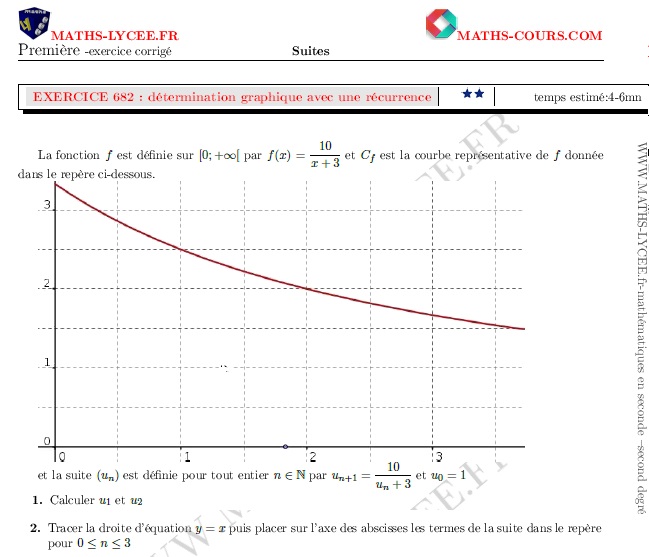
	réf 682-Détermination graphique des termes d'une suite définie par récurrence aperçu exercice nº 682 Détermination graphique des termes d'une suite définie par récurrence Ouvrir l'exercice	\| \| \|	- calcul des premiers termes - détermination graphique des premiers termes
série 3	Variations
niveau	Titre	infos	contenu
	réf 684-Étude des variations d'une suite aperçu exercice nº 684 Étude des variations d'une suite Ouvrir l'exercice	\| \| \|	- étude des variations avec une forme explicite - fonction associée
	réf 683-Étude des variations avec une forme explicte aperçu exercice nº 683 Étude des variations avec une forme explicte Ouvrir l'exercice	\| \| \|	- étude des variations d'une suite - signe de la différence de deux termes consécutifs
	réf 685-Étude des variations avec la fonction associée aperçu exercice nº 685 Étude des variations avec la fonction associée Ouvrir l'exercice	\| \|	- variations d'une fonction - dérivée d'une fonction - formules de dérivations (produit, quotient)
	réf 686-Étude des variations aperçu exercice nº 686 Étude des variations Ouvrir l'exercice	\| \|	- étude des variations avec la fonction associée - étude du signe de la différence de deux termes consécutifs
	réf 687-Variations d'une suite géométrique aperçu exercice nº 687 Variations d'une suite géométrique Ouvrir l'exercice	\| \|	- forme explicite d'une suite géométrique - étude des variations suite géométrique
série 4	Limites
niveau	Titre	infos	contenu
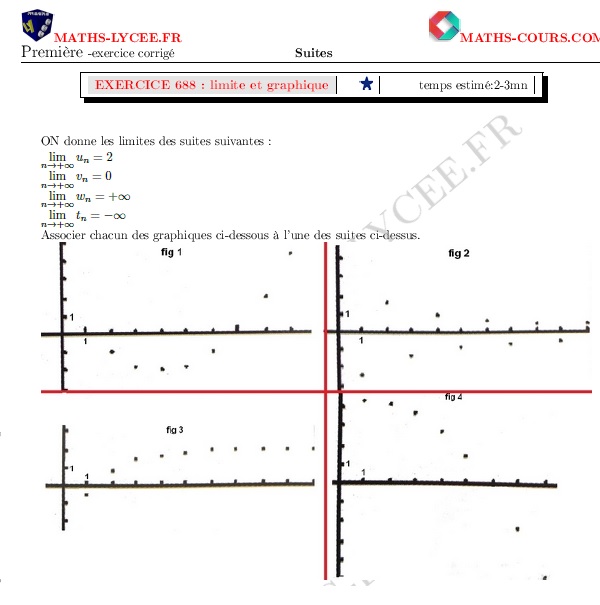
	réf 688-Lien limite et représentation graphique d'une suite aperçu exercice nº 688 Lien limite et représentation graphique d'une suite Ouvrir l'exercice	\| \|	identifier la représentation graphique d'une suite avec la limite des suites
	réf 689-Limite avec une forme explicite aperçu exercice nº 689 Limite avec une forme explicite Ouvrir l'exercice	\| \|	- déterminer intuitivement une limite avec une forme explicite
	réf 690-Limite avec une relation de récurrence et calculatrice aperçu exercice nº 690 Limite avec une relation de récurrence et calculatrice Ouvrir l'exercice	\| \|	- recherche d'une limite avec la calculatrice
	réf 691-Calcul de la limite d'une suite définie par un polynôme de degré 2 aperçu exercice nº 691 Calcul de la limite d'une suite définie par un polynôme de degré 2 Ouvrir l'exercice	\| \|	- limite d'un produit - limite d'un polynôme de degré 2
	réf 692-Limite avec un quotient aperçu exercice nº 692 Limite avec un quotient Ouvrir l'exercice	\| \|	- limite avec un quotient - recherche avec la calculatrice - recherche par le calcul
	réf 693-Recherche d'une limite aperçu exercice nº 693 Recherche d'une limite Ouvrir l'exercice	\| \|	- étude des variations - conjecturer une limite - prouver la conjecture faite
série 5	Suites arithmétiques
niveau	Titre	infos	contenu
	réf 695-Calculs des termes d'une suite arithmétique aperçu exercice nº 695 Calculs des termes d'une suite arithmétique Ouvrir l'exercice	\| \| \|	- calcul de $u_1$ et $u_2$ - expression de $u_n$ en fonction de $n$
	réf 696-Déterminer si une suite est arithmétique aperçu exercice nº 696 Déterminer si une suite est arithmétique Ouvrir l'exercice	\| \| \|	- calcul des termes d'une suite - justifier qu'une suite n'est pas arithmétique - justifier qu'une suite est arithmétique
	réf 697-Montrer qu'une suite est arithmétique aperçu exercice nº 697 Montrer qu'une suite est arithmétique Ouvrir l'exercice	\| \| \|	- justifier qu'une suite est arithmétique et déterminer sa raison
	réf 698-Déterminer si une suite est arithmétique aperçu exercice nº 698 Déterminer si une suite est arithmétique Ouvrir l'exercice	\| \| \|	- identifier une suite arithmétique - montrer que $u_n$ est ou n'est pas arithmétique
	réf 699-Calcul de la raison d'une suite arithmétique aperçu exercice nº 699 Calcul de la raison d'une suite arithmétique Ouvrir l'exercice	\| \| \|	- calcul de la raison connaissant deux termes de la suite - calcul du premier terme
	réf 700-Problème utilisant une suite arithmétique aperçu exercice nº 700 Problème utilisant une suite arithmétique Ouvrir l'exercice	\| \|	- forme explicite d'une suite arithmétique - - recherche d'un seuil
	réf 701-Problème utilisant une suite arithmétique aperçu exercice nº 701 Problème utilisant une suite arithmétique Ouvrir l'exercice	\| \|	- placement et ajout d'une somme chaque année - forme explicite d'une suite arithmétique - recherche d'un seuil
	réf 702-Somme des termes d'une suite arithmétique aperçu exercice nº 702 Somme des termes d'une suite arithmétique Ouvrir l'exercice	\| \|	- calcul de la somme des termes connaissant le premier terme et la raison
	réf 703-Somme utilisant une suite arithmétique aperçu exercice nº 703 Somme utilisant une suite arithmétique Ouvrir l'exercice	\| \|	- identifier une suite arithmétique - calculer une somme des termes d'une suite arithmétique
série 6	Suites géométriques
niveau	Titre	infos	contenu
	réf 705-Calcul des termes d'une suite géométrique aperçu exercice nº 705 Calcul des termes d'une suite géométrique Ouvrir l'exercice	\| \|	- calcul des termes en utilisant la forme explicite
	réf 706-Calcul des termes d'une suite géométrique aperçu exercice nº 706 Calcul des termes d'une suite géométrique Ouvrir l'exercice	\| \|	- utilisation de la relation $u_n=u_n\times q^{n-p}$
	réf 707-Suite géométrique de premier terme $u_1$ aperçu exercice nº 707 Suite géométrique de premier terme $u_1$ Ouvrir l'exercice	\| \|	- calcul des termes et forme explicite d'une suite géométrique de premier terme $u_1$
	réf 708-Déterminer si une suite est géométrique aperçu exercice nº 708 Déterminer si une suite est géométrique Ouvrir l'exercice	\| \|	- reconnaître l'expression d'une suite géométrique - calcul du quotient de deux termes consécutifs - calculs avec des exposants
	réf 709-Déterminer la raison d'une suite géométrique aperçu exercice nº 709 Déterminer la raison d'une suite géométrique Ouvrir l'exercice	\| \|	- déterminer la raison d'une suite géométrique connaissant deux termes de cette suite - déterminer le premier terme et exprimer un en fonction de n (forme explicite)
	réf 710-Variations d'une suite géométrique aperçu exercice nº 710 Variations d'une suite géométrique Ouvrir l'exercice	\| \|	- expression de un en fonction de n (forme explicite d'une suite géométrique) - calcul de la différence de deux termes consécutifs - signe de un+1 -un et variations de la suite
	réf 743-Placement à intérêts composés aperçu exercice nº 743 Placement à intérêts composés Ouvrir l'exercice	\| \| \|	- pourcentage d'augmentation - suite géométrique - forme explicite d'une suite géométrique
	réf 711-Application des suites géométriques aperçu exercice nº 711 Application des suites géométriques Ouvrir l'exercice	\| \|	- augmentation d'un pourcentage donné - montrer qu'une suite est géométrique - déterminer l'expression de un en fonction de n (forme explicite) - déterminer les variations d'une suite géométrique - recherche d'un seuil avec la calculatrice
	réf 712-Application des suites géométriques (extrait bac 2015) aperçu exercice nº 712 Application des suites géométriques (extrait bac 2015) Ouvrir l'exercice	\| \|	- justifier qu'une suite géométrique - recherche de la forme explicite - lecture d'un algorithme et le compléter(recherche d'un seuil) - étude des variations
	réf 713-Calcul de la somme des termes d'une suite géométrique aperçu exercice nº 713 Calcul de la somme des termes d'une suite géométrique Ouvrir l'exercice	\| \|	somme des termes d'une suite géométrique
	réf 714-Calculer une somme de nombres en utilisant une suite géométrique aperçu exercice nº 714 Calculer une somme de nombres en utilisant une suite géométrique Ouvrir l'exercice	\| \|	- identification d'une suite géométrique et de sa raison - somme de nombres en utilisant une suite géométrique
série 8	Algorithmes
niveau	Titre	infos	contenu
	réf 715-Lecture de trois algorithmes (extrait bac) aperçu exercice nº 715 Lecture de trois algorithmes (extrait bac) Ouvrir l'exercice	\| \|	- déterminer le résultat donné par un algorithme - affichage des termes et recherche d'un seuil
	réf 716-Algorithme avec une boucle POUR en Python aperçu exercice nº 716 Algorithme avec une boucle POUR en Python Ouvrir l'exercice	\| \|	- calcul des termes d'une suite définie par récurrence - écriture d'un algorithme en Python
	réf 718-Recherche d'un seuil avec une suite géométrique aperçu exercice nº 718 Recherche d'un seuil avec une suite géométrique Ouvrir l'exercice	\| \|	- suite géométrique et forme explicite - lecture d'un programme en Python - contrôle du résultat affiché
	réf 717-Recherche d'un seuil aperçu exercice nº 717 Recherche d'un seuil Ouvrir l'exercice	\| \|	- boucle TANT QUE - recherche d'un seuil pour les termes d'une suite - programmation en Python
	réf 744-Suite de Syracuse aperçu exercice nº 744 Suite de Syracuse Ouvrir l'exercice	\| \|	- lecture et programmation d'un algorithme en Python - modification de l'algorithme et test
série 9	Exercices de synthèse
niveau	Titre	infos	contenu
	réf 720-Comparaison de deux suites aperçu exercice nº 720 Comparaison de deux suites Ouvrir l'exercice	\| \|	- justifier qu'une suite est arithmétique - donner la forme explicite - justifier qu'une suite est géométrique - donner la forme explicite - comparaison des termes des deux suites
	réf 719-Comparaison de deux suites aperçu exercice nº 719 Comparaison de deux suites Ouvrir l'exercice	\| \|	- justifier qu'une suite est arithmétique - forme explicite d'une suite arithmétique - justifier qu'une suite est géométrique - forme explicite d'une suite géométrique - comparaison des termes des deux suites - somme des termes d'une suite arithmétique - somme des termes d'une suite géométrique
	réf 721-Suites et algorithme aperçu exercice nº 721 Suites et algorithme Ouvrir l'exercice	\| \|	- suite arithmétique - suite géométrique - recherche d'un seuil avec un algorithme - calcul des termes d'une suite avec la calculatrice
	réf 722-Suite arithmético-géométrique (relation de la forme $u_{n +1}=au_n +b$) aperçu exercice nº 722 Suite arithmético-géométrique (relation de la forme $u_{n +1}=au_n +b$) Ouvrir l'exercice	\| \| \|	- justifier qu'une suite n'est ni arithmétique, ni géométrique - utilisation d'une suite auxiliaire géométrique - recherche de la forme explicite - calcul d'un terme et contrôle avec la calculatrice
	réf 723-Suite de la forme $u_{n+1}=au_n+b$ aperçu exercice nº 723 Suite de la forme $u_{n+1}=au_n+b$ Ouvrir l'exercice	\| \| \|	- algorithme - suite de la forme un+1=aun+b (suite arithmético-géométrique) - suite géométrique associée - forme explicite d'une suite géométrique - comportement à l'infini (limite)
	réf 724-Suites (BAC S 2012) aperçu exercice nº 724 Suites (BAC S 2012) Ouvrir l'exercice	\| \|	- suite de points sur un axe gradué - suite arithmético géométrique: forme $u_{n+1}=au_n+b$ - suite géométrique associée - recherche de la forme explicite - limite d'une suite
	réf 725-Suites BAC S 2010 aperçu exercice nº 725 Suites BAC S 2010 Ouvrir l'exercice	\| \|	- suites liées - suites arithmétiques - somme des termes d'une suite
	réf 726-Suites liées (BAC S 2006) aperçu exercice nº 726 Suites liées (BAC S 2006) Ouvrir l'exercice	\| \|	- calcul de coordonnées avec une relation vectorielle - suites liées - montrer qu'une suite est géométrique - étude des variations d'une suite
	réf 727-Suites liées par une relation de récurrence aperçu exercice nº 727 Suites liées par une relation de récurrence Ouvrir l'exercice	\| \|	- suites liées par une relation de récurrence et recherche de la forme explicite de chacune des suites - suites géométriques
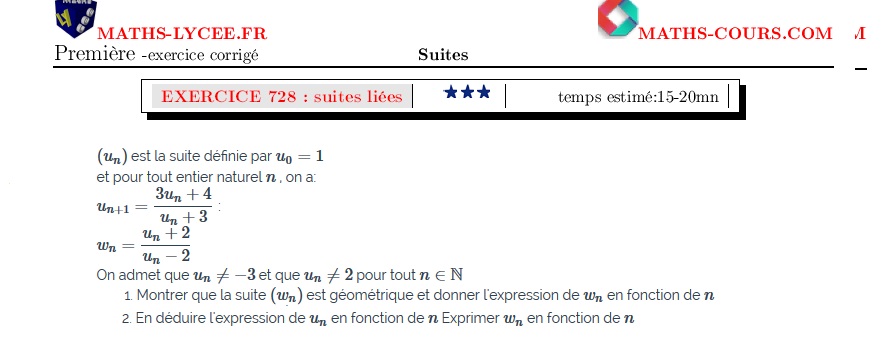
	réf 728-Suites liées par une relation de récurrence aperçu exercice nº 728 Suites liées par une relation de récurrence Ouvrir l'exercice	\| \|	Suites liées par une relation Recherche de la forme explicite de chacune des suites - suites géométriques
	réf 729-Suites liées- suites arithmétiques aperçu exercice nº 729 Suites liées- suites arithmétiques Ouvrir l'exercice	\| \|	- Suite non arithmétique définie par une relation de récurrence - Suite associée - Forme explicite de un
	réf 730-Suites liées- suites arithmétiques aperçu exercice nº 730 Suites liées- suites arithmétiques Ouvrir l'exercice	\| \|	- Suite définie par une relation de récurrence (racine carrée) - Calcul des premiers termes - Suite arithmétique associée - Recherche de la forme explicite
	réf 731-Problème ouvert aperçu exercice nº 731 Problème ouvert Ouvrir l'exercice	\| \|	- suite arithmétique - somme des termes d'une suite arithmétique
	réf 732-Problème ouvert aperçu exercice nº 732 Problème ouvert Ouvrir l'exercice	\| \|	- problème utilisant une suite géométrique
	réf 1462-Complexes et suites (d'après BAC S) aperçu exercice nº 1462 Complexes et suites (d'après BAC S) Ouvrir l'exercice	\| \|	- forme exponentielle - suite géométrique - limite d'une suite géométrique
	réf 1463-Suites et complexes d'après BAC S aperçu exercice nº 1463 Suites et complexes d'après BAC S Ouvrir l'exercice	\| \|	- forme trigonométrique - suite géométrique - algorithme
	réf 1599-Suites liées et suite arithmético-géométrique aperçu exercice nº 1599 Suites liées et suite arithmético-géométrique Ouvrir l'exercice	\| \|	- suite de la forme $u_{n+1}=au_n+b$ - étude des variations et limite
	CONTRÔLES CORRIGÉS
niveau	Titre	infos	contenu
	réf 733-Interrogation suites et variations	\| \|	- forme explicite - relation de récurrence - étude des variations
	réf 734-Interrogation niv 1 suites arithmétiques et géométriques	\| \|	- relation de récurrence et forme explicite : - suites arithmétiques - suites géométriques
	réf 735-Devoir complet suites arithmétiques et géométriques	\| \|	- variations d'une suite - suite arithmétique -suite géométrique
	réf 736-Devoir complet fiin de chapitre niv 3	\| \|	- variations d'une suite - suites arithmétiques et géométriques - somme des termes d'une suite - algorithme

Publications MATHS-LYCEE.FR

mémo+exercices corrigés+liens vidéos

chapitre 3 Suites

En mode visiteur, vous ne disposez pas des fonctionnalités du site (documents vus, à revoir, validés, conseillés...)

92 documents pour le chapitre 3 Suites

COURS

AIDE MÉMOIRE

MÉTHODES

QCM

VIDÉOS

EXERCICES

Démonstrations de cours

Calculs des termes

Variations

Limites

Suites arithmétiques

Suites géométriques

Algorithmes

Exercices de synthèse

CONTRÔLES CORRIGÉS

mémo+exercices corrigés+liens vidéos

chapitre 3 Suites

En mode visiteur, vous ne disposez pas des fonctionnalités du site (documents vus, à revoir, validés, conseillés...)

92 documents pour le chapitre 3 Suites

Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez! Un cours particulier à la demande!

COURS

AIDE MÉMOIRE

MÉTHODES

QCM

VIDÉOS

EXERCICES

Démonstrations de cours

exercice nº 748 Somme des entiers naturels

exercice nº 754 Somme des termes d'une suite géométrique

Calculs des termes

exercice nº 674 Calcul des termes avec une forme explicite

exercice nº 675 Reconnaître une forme explicite ou une récurrence

exercice nº 676 Suite définie par récurrence

exercice nº 678 Suite définie par récurrence

exercice nº 677 Travail avec les indices (forme explicite)

exercice nº 679 Suites liées

exercice nº 680 Calculs sur les indices-suites liées

exercice nº 681 Détermination graphique avec une forme explicite

exercice nº 682 Détermination graphique des termes d'une suite définie par récurrence

Variations

exercice nº 684 Étude des variations d'une suite

exercice nº 683 Étude des variations avec une forme explicte

exercice nº 685 Étude des variations avec la fonction associée

exercice nº 686 Étude des variations

exercice nº 687 Variations d'une suite géométrique

Limites

exercice nº 688 Lien limite et représentation graphique d'une suite

exercice nº 689 Limite avec une forme explicite

exercice nº 690 Limite avec une relation de récurrence et calculatrice

exercice nº 691 Calcul de la limite d'une suite définie par un polynôme de degré 2

exercice nº 692 Limite avec un quotient

exercice nº 693 Recherche d'une limite

Suites arithmétiques

exercice nº 695 Calculs des termes d'une suite arithmétique

exercice nº 696 Déterminer si une suite est arithmétique

exercice nº 697 Montrer qu'une suite est arithmétique

exercice nº 698 Déterminer si une suite est arithmétique

exercice nº 699 Calcul de la raison d'une suite arithmétique

exercice nº 700 Problème utilisant une suite arithmétique

exercice nº 701 Problème utilisant une suite arithmétique

exercice nº 702 Somme des termes d'une suite arithmétique

exercice nº 703 Somme utilisant une suite arithmétique

Suites géométriques

exercice nº 705 Calcul des termes d'une suite géométrique

exercice nº 706 Calcul des termes d'une suite géométrique

exercice nº 707 Suite géométrique de premier terme $u_1$

exercice nº 708 Déterminer si une suite est géométrique

exercice nº 709 Déterminer la raison d'une suite géométrique

exercice nº 710 Variations d'une suite géométrique

exercice nº 743 Placement à intérêts composés

exercice nº 711 Application des suites géométriques

exercice nº 712 Application des suites géométriques (extrait bac 2015)

exercice nº 713 Calcul de la somme des termes d'une suite géométrique

exercice nº 714 Calculer une somme de nombres en utilisant une suite géométrique

Algorithmes

exercice nº 715 Lecture de trois algorithmes (extrait bac)

exercice nº 716 Algorithme avec une boucle POUR en Python

exercice nº 718 Recherche d'un seuil avec une suite géométrique

exercice nº 717 Recherche d'un seuil

exercice nº 744 Suite de Syracuse

Exercices de synthèse

exercice nº 720 Comparaison de deux suites

exercice nº 719 Comparaison de deux suites

exercice nº 721 Suites et algorithme

exercice nº 722 Suite arithmético-géométrique (relation de la forme $u_{n +1}=au_n +b$)

exercice nº 723 Suite de la forme $u_{n+1}=au_n+b$

exercice nº 724 Suites (BAC S 2012)

exercice nº 725 Suites BAC S 2010

exercice nº 726 Suites liées (BAC S 2006)

exercice nº 727 Suites liées par une relation de récurrence

exercice nº 728 Suites liées par une relation de récurrence

exercice nº 729 Suites liées- suites arithmétiques

exercice nº 730 Suites liées- suites arithmétiques

exercice nº 731 Problème ouvert

exercice nº 732 Problème ouvert