Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
Dans les classes de première d'un lycée, les élèves peuvent choisir en option les langues suivantes:
-Espagnol
-Allemand
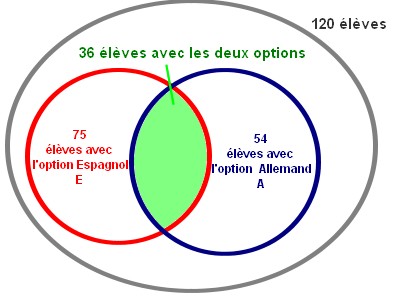
Parmi les 120 élèves de première, 75 ont choisi l'espagnol et 54 l'allemand.
36 élèves ont choisi les deux langues en option. On note $E$ l'événement "l'élève a choisi l'option Espagnol" et $A$ l'événement "l'élève a choisi l'option Allemand".
On choisit un élève de première au hasard.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
-Espagnol
-Allemand
Parmi les 120 élèves de première, 75 ont choisi l'espagnol et 54 l'allemand.
36 élèves ont choisi les deux langues en option. On note $E$ l'événement "l'élève a choisi l'option Espagnol" et $A$ l'événement "l'élève a choisi l'option Allemand".
On choisit un élève de première au hasard.
- Construire un diagramme illustrant cette situation(diagramme de Venn).
- $p(E)$
Probabilité avec une loi équirépartie
Dans le cas d'une loi équirépartie, la probabilité d'un événement A est $p(A)=\dfrac{\text{nombre de cas favorables}}{\text{nombre de cas possibles}}$$p(E)=\dfrac{75}{120}=0,625$
- $p(E\cap A)$
Intersection (A et B) et réunion (A ou B)
Soient A et B deux événements.
L'événement $A \cap B$ (lire A inter B) est l'ensemble des issues qui réalisent à la fois A et B.
Si $A \cap B =\oslash$, on dit que A et B sont incompatibles.
L'événement $A \cup B$ (lire A union B) est l'ensemble des issues qui réalisent A ou bien B, c'est à dire réalisant A ou bien réalisant B ou bien réalisant A et B.
$p(A\cup B)=p(A)+p(B)-p(A\cap B)$On a 37 élèves qui ont choisi les deux langues en option.37 élèves ont choisi les deux langues en option
$p(E\cap A)=\dfrac{36}{120}=0,3$
- $p(E\cup A)$
il ne faut pas compter deux fois les élèves ayant choisi les deux options.
75 ont choisi l'espagnol mais parmi ceux-ci, il peut y avoir des élèves ayant aussi choisi l'option Allemand.
$p(E\cup A)=p(E)+p(A)-p(E\cap A)$
$\phantom{p(E\cup A)}=0,625+\dfrac{54}{120}-0,3$
$\phantom{p(E\cup A)}=0,625+0,45-0,3$
$\phantom{p(E\cup A)}=0,775$
- $p(\overline{E\cup A})$
$E\cup A$ est l'événement correspondant aux trois cas suivants:
- l'élève a choisi seulement l'option Espagnol
- l'élève a choisi seulement l'option Allemand
- l'élève a choisi les deux options$E\cup A$ est l'événement correspondant aux trois cas suivants:
- l'élève a choisi seulement l'option Espagnol
- l'élève a choisi seulement l'option Allemand
- l'élève a choisi les deux options
$\overline{E\cup A}$ est l'événement contraire de $E\cup A$ (donc ne correspond à aucune des situations ci-dessus)
donc $\overline{E\cup A}$ est l'événement "l'élève n'a choisi aucune de ces deux options".
En utilisant le diagramme, on a:
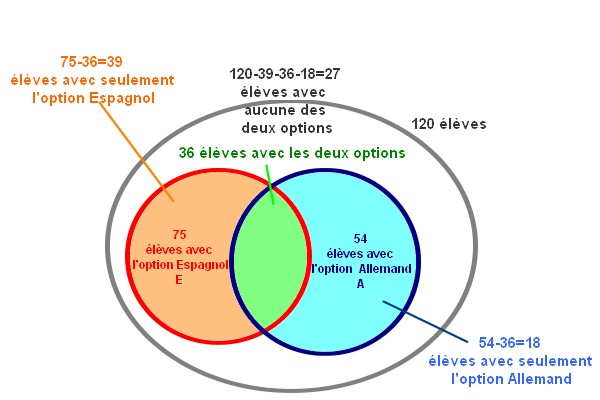
$p(\overline{E\cup A})=\dfrac{27}{120}=0,225$
Calculer les probabilités suivantes et en donner la signification (on pourra éventuellement s'aider du diagramme):
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
vidéos semblables
Pour compléter cet exercice, nous vous conseillons les vidéos suivantes semblables à l'exercice affiché.
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.