Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
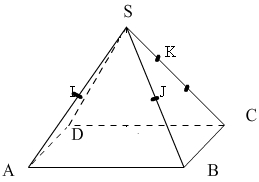
$ABCDS$ est une pyramide à base carrée de sommet $S$ et $I$ et $J$ sont les milieux respectifs de $[SA]$ et $[SB]$.
$K$ est le point défini par la relation $\overrightarrow{SK}=\dfrac{1}{3}\overrightarrow{SC}$.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
$K$ est le point défini par la relation $\overrightarrow{SK}=\dfrac{1}{3}\overrightarrow{SC}$.
- Faire ne figure.
produit d'un vecteur par un réel
Soit un réel $k\neq 0$ et un vecteur $\overrightarrow{u}\neq \overrightarrow{0}$
Le produit de $k$ par le vecteur $\overrightarrow{u}$ est le vecteur $k\overrightarrow{u}$ tel que:
1. $k\overrightarrow{u}$ et $\overrightarrow{u}$ ont la même direction
2. $k\overrightarrow{u}$ et $\overrightarrow{u}$ ont le même sens si $k>0$ et des sens contraires si $k <0$
3. $||k\overrightarrow{u}||=|k| \times ||\overrightarrow{u}||$
Si $k=0$ ou $\overrightarrow{u}=\overrightarrow{0}$ alors $k\overrightarrow{u}=\overrightarrow{0}$.
- Montrer que les droites $(IJ)$ et $(CD)$ sont parallèles.
vecteurs colinéaires
Deux vecteurs non nuls $\overrightarrow{u}$ et $\overrightarrow{w}$ sont colinéaires si et seulement si il existe un réel $k\neq 0$ tel que $\overrightarrow{w}=k\overrightarrow{u}$On peut montrer que les vecteurs directeurs sont colinéairesDans le triangle $ABCS$ on a $I$ milieu de $[SA]$ et $J$ milieu de $[SB]$ donc $\overrightarrow{IJ}=\dfrac{1}{2}\overrightarrow{DC}$
donc $\overrightarrow{IJ}=\dfrac{1}{2}\overrightarrow{DC}$
donc les vecteurs directeurs des droites $(IJ)$ et $(CD)$ sont colinéaires
- Montrer que les droites $(JK)$ et $(BC)$ ne sont pas parallèles.
$\overrightarrow{JK}=\overrightarrow{JS}+\overrightarrow{SK}$
donc $\overrightarrow{JK}=\dfrac{1}{2}\overrightarrow{BS}+\dfrac{1}{3}\overrightarrow{SC}$
et $\overrightarrow{BC}=\overrightarrow{BS}+\overrightarrow{SC}$
Il n'existe donc pas de réel $k$ tel que $\overrightarrow{JK}=k\overrightarrow{BC}$
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
