MATHS-LYCEE.FR exercice corrigé chapitre Produit scalaire

Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.
*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)

PDF reservé aux abonnés

On donne trois points $A$, $B$ et $C$ du plan.

Calculer $ \overrightarrow{AB}. \overrightarrow{AC}$ sachant que tels que $AB=4$ et $AC=6$ unités.

Rappel de cours

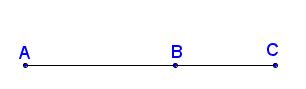
Produit scalaire (définition)
$\overrightarrow{u}$ et $\overrightarrow{v}$ sont deux vecteurs non nuls tels que $\overrightarrow{u}=\overrightarrow{AB}$ et $\overrightarrow{v}=\overrightarrow{AC}$, le produit scalaire des deux vecteurs est noté $\overrightarrow{u}.\overrightarrow{v}$,et est le nombre réel défini par:
$\overrightarrow{u}.\overrightarrow{v}=\mid \mid \overrightarrow{u}\mid \mid\times \mid \mid \overrightarrow{v}\mid \mid \times cos(\widehat{BAC})=AB\times AC\times cos(\widehat{BAC})$

Aide

$B\in [AC]$ donc $\widehat{BAC}=0$

Solution

figure

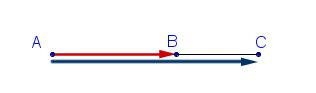
$B\in [AB]$ donc $( \overrightarrow{AB}, \overrightarrow{AC})=0+k2\pi$ avec $k\in \mathbb{Z}$
$ \overrightarrow{AB}. \overrightarrow{AC}=|| \overrightarrow{AB}||\times || \overrightarrow{AC}||\times cos( \overrightarrow{AB}, \overrightarrow{AC})$
$\phantom{ \overrightarrow{AB}. \overrightarrow{AC}}=AB\times AC \times cos(0)$
$\phantom{ \overrightarrow{AB}. \overrightarrow{AC}}=4\times 6 \times 1$
$\phantom{ \overrightarrow{AB}. \overrightarrow{AC}}=24$
Calculer $ \overrightarrow{AB}. \overrightarrow{AC}$ sachant que tels que $AB=4$, $AC=6$ et $BC=2$ unités.

Rappel de cours

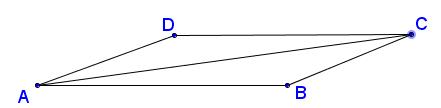
Produit scalaire avec les normes
Pour tous vecteurs $\overrightarrow{u}=\overrightarrow{AB}$ et $\overrightarrow{v}=\overrightarrow{AC}$ on a:
$\overrightarrow{u}.\overrightarrow{v}=\dfrac{\mid \mid \overrightarrow{u}\mid \mid^2+\mid \mid \overrightarrow{v}\mid \mid^2-\mid \mid \overrightarrow{u}-\overrightarrow{v}\mid \mid^2}{2}$
Dans le triangle $ABC$: $\overrightarrow{AB}.\overrightarrow{AC}=\dfrac{AB^2+AC^2-BC^2}{2}$

Aide

Utiliser les côtés du triangle ABC

Solution

figure

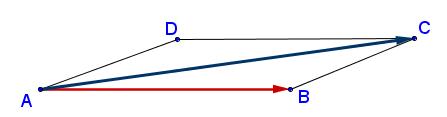
$\overrightarrow{AB}.\overrightarrow{AC}=\dfrac{AB^2+AC^2-BC^2}{2}$
$\phantom{\overrightarrow{AB}.\overrightarrow{AC}}=\dfrac{4^2+6^2-2^2}{2}$
$\phantom{\overrightarrow{AB}.\overrightarrow{AC}}=\dfrac{16+36-4}{2}$
$\phantom{\overrightarrow{AB}.\overrightarrow{AC}}=24$
Calculer $ \overrightarrow{AB}. \overrightarrow{AC}$ tels que $AB=6$, $AC=4$ unités et $\widehat{BAC}=30^0$.

Rappel de cours

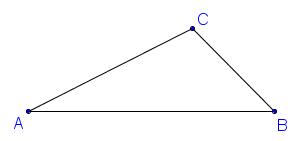
Produit scalaire (définition)
$\overrightarrow{u}$ et $\overrightarrow{v}$ sont deux vecteurs non nuls tels que $\overrightarrow{u}=\overrightarrow{AB}$ et $\overrightarrow{v}=\overrightarrow{AC}$, le produit scalaire des deux vecteurs est noté $\overrightarrow{u}.\overrightarrow{v}$,et est le nombre réel défini par:
$\overrightarrow{u}.\overrightarrow{v}=\mid \mid \overrightarrow{u}\mid \mid\times \mid \mid \overrightarrow{v}\mid \mid \times cos(\widehat{BAC})=AB\times AC\times cos(\widehat{BAC})$

Solution

figure

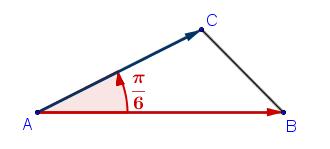
$30^0$ correspondent à $\dfrac{\pi}{6}$ radians
et $cos(\dfrac{\pi}{6})=\dfrac{\sqrt{3}}{2}$
$ \overrightarrow{AB}. \overrightarrow{AC}=|| \overrightarrow{AB}||\times || \overrightarrow{AC}||\times cos( \widehat{BAC})$
$\phantom{ \overrightarrow{AB}. \overrightarrow{AC}}=AB\times AC \times cos(\dfrac{\pi}{6})$
$\phantom{ \overrightarrow{AB}. \overrightarrow{AC}}=6\times 4 \times \dfrac{\sqrt{3}}{2}$
$\phantom{ \overrightarrow{AB}. \overrightarrow{AC}}=\dfrac{24\sqrt{3}}{2}$
Calculer $ \overrightarrow{AB}. \overrightarrow{AC}$ tels que $AB=6$, $AC=BC=4$ unités.

Rappel de cours

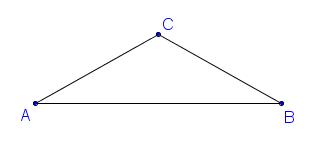include156

Aide

Construire le projeté orthogonal de C sur $(AB)$
Le triangle ABC est équilatéral donc la hauteur issue de C est confondue avec la médiane issue de C dans ABC.

Solution

Soit $H$ le projeté orthogonal de $C$ sur $(AB)$(voir figure)

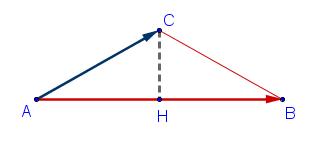
Le triangle ABC est isocèle en C donc la hauteur (AH) issue de C est confondue avec la médiane issue de C dans ABC.
donc $H$ est le milieu de $[AB]$
On a $\widehat{BAC}=\dfrac{\pi-\widehat{ACB}}{2}$
donc la mesure de l'angle $\widehat{BAC}$ est inférieure à $\dfrac{\pi}{2}$ radians
$\widehat{BAC}$ est donc un angle aigu donc $ \overrightarrow{AB}. \overrightarrow{AC}$ est positif

$ \overrightarrow{AB}. \overrightarrow{AC}=AB\times AH$
$\phantom{ \overrightarrow{AB}. \overrightarrow{AC}}=6\times 3$
$\phantom{ \overrightarrow{AB}. \overrightarrow{AC}}=18$

On peut aussi utiliser:
$\overrightarrow{AB}.\overrightarrow{AC}=\dfrac{AB^2+AC^2-BC^2}{2}$
$\phantom{\overrightarrow{AB}.\overrightarrow{AC}}=\dfrac{6^2+4^2-4^2}{2}$
$\phantom{\overrightarrow{AB}.\overrightarrow{AC}}=\dfrac{6^2}{2}$
$\phantom{\overrightarrow{AB}.\overrightarrow{AC}}=18$