Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
On considère le demi-cercle de diamètre $[AB]$ avec $AB=10$ cm et le point $C$ est un point du demi-cercle.
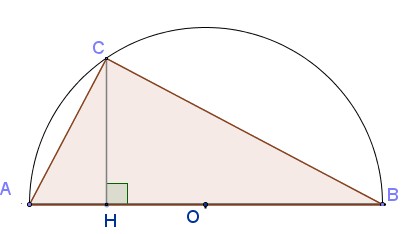
On note $AH=x$
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)

On note $AH=x$
- Exprimer $CH$ en fonction de $x$.
On distinguera les cas $x\leq 5 $ ET $x>5$
On peut utiliser le triangle $OCH$ rectangle en $H$.Dans le triangle $OCH$ rectangle en $H$, on a $OC^2=OH^2+HC^2$
Premier cas: $H\in [AO]$ soit $x\in[0;5]$
Dans ce cas, $OH=5-x$, donc on a:
$5^2=(5-x)^2+HC^2$
donc $HC^2=25-(5-x)^2=25-(25-10x+x^2)=25-25+10x-x^2=10x-x^2$
et $HC=\sqrt{10x-x^2}$
Deuxième cas: $H\in [OB]$ soit $x\in[5;10]$
Dans ce cas, $OH=x-5$, donc on a:
$5^2=(x-5)^2+HC^2$
donc $HC^2=25-(x-5)^2=25-(x^2-10x+25)=25-x^2+10x-25=10x-x^2$
et $HC=\sqrt{10x-x^2}$
donc dans les deux cas, on trouve $HC=\sqrt{10x-x^2}$.
- On note $A$ la fonction qui à $x$ associe l'aire du triangle $ABC$.
Quel est l'ensemble de définition de la fonction $A$?
Exprimer $A(x)$ en fonction de $x$.Le point $H\in [AB]$.
Rappel: l'aire d'un triangle est $A=\dfrac{\text{base}\times \text{hauteur}}{2}$Le point $H$ est un point du segment $[AB]$ avec $AB=10$ et $x=AH$
donc $0 \leq x \leq 10$
La hauteur issue de $C$ dans le triangle $ABC$ est $(CH)$ donc on a:
$A(x)=\dfrac{AB\times CH}{2}=\dfrac{10\times \sqrt{10x-x^2}}{2}=5 \sqrt{10x-x^2}$
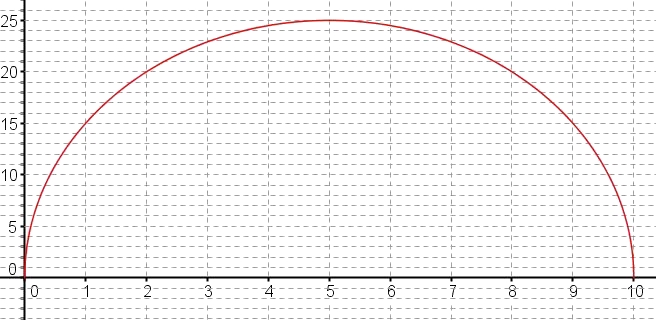
- En utilisant la calculatrice, conjecturer(émettre une hypothèse sans la prouver) la position de $C$ pour laquelle l'aire du triangle est maximale.
On peut utiliser le MENU TABLE de la calculatrice.Dans le MENU TABLE, en saisissant l'expression de $A(x)$ dans Y1 et en paramétrant dans SET XMIN=0, XMAX=10 et STEP=0,1 par exemple, on obtient:

Il semble donc que l'aire maximale soit de 25 cm$^2$ atteinte pour $x=5$ c'est à dire lorsque $H$ est confondu avec $O$.
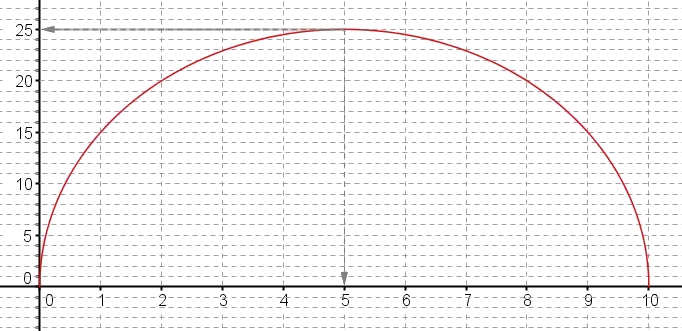
- On donne ci-dessous la représentation graphique de la fonction $A$.
Vérifier que la conjecture émise à la question précédente est cohérente avec le graphique.On a représenté l'aire en fonction de $x$:
- Déterminer le nombre de positions du point $C$ pour lesquelles l'aire du triangle est de 15 cm$^2$.
Contrôler les solutions obtenues par le calcul.On cherche le nombre de points de la courbe ayant une ordonnée égale à 15.On veut résoudre graphiquement $A(x)=15$.
Les solutions de l'équation $A(x)=15$ sont les abscisses des points d'intersection de la courbe et de la droite d'équation $y=15$ (en bleu sur le graphique).
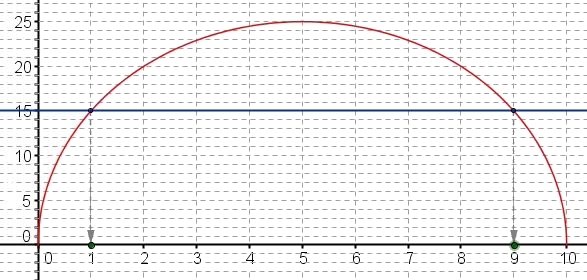
donc $A(x)=15$ pour $x=1$ ou pour $x=9$.
En calculant l'image de $1$ puis celle de $9$ par la fonction $A$, on a:
$A(1)=5\sqrt{10-1^2}=5\times 3=15$ et $A(9)=5\times \sqrt{10\times 9-9^2}=5\times 3=15$
- En déduire graphiquement les positions possibles du point $C$ pour lesquelles l'aire du triangle est inférieure ou égale à 15 cm$^2$.
Il faut déterminer les abscisses des points de la courbe dont l'ordonnée est inférieure ou égale à 15.On veut résoudre l'inéquation $A(x)\leq 15$.
Graphiquement, les solutions sont les abscisses des points de la courbe (en pointillés bleus sur le graphique) situés en-dessous de la droite d'équation $y=15$ (en bleu sur le graphique)
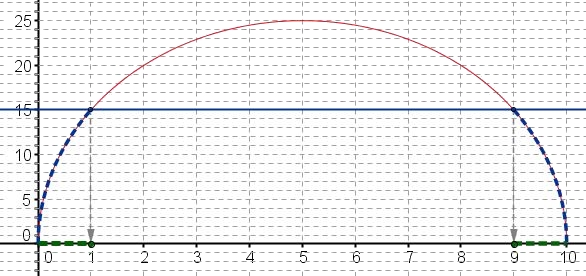
donc $A(x)\leq 15$ pour $x\in [0;1]$ ou pour $x\in [9;10]$.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
