Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
Dans une ville, il peut venter, neiger ou grêler.
Le vent et la grêle ne restent jamais deux jours de suite.
S'il vente un jours donné, le lendemain il neige ou il grêle de manière équiprobable.
S'il neige un jours donné, il y a une chance sur 3 qu'il vente le lendemain et une chance sur deux qu'il continue à neiger le lendemain.
Après un jour de grêle il y a deux fois plus de chance d'avoir de la neige que du vent.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Le vent et la grêle ne restent jamais deux jours de suite.
S'il vente un jours donné, le lendemain il neige ou il grêle de manière équiprobable.
S'il neige un jours donné, il y a une chance sur 3 qu'il vente le lendemain et une chance sur deux qu'il continue à neiger le lendemain.
Après un jour de grêle il y a deux fois plus de chance d'avoir de la neige que du vent.
- Justifier que l'on peut modéliser cette situation par une chaîne de Markov à trois états et donner son graphe probabiliste.
Chaîne de Markov
On considère une suite de variables aléatoires $(X_n)$ définies sur un même espace fini muni d'une probabilité.
On dit que $X_n$ est une chaîne de Markov à deux états $A$ et $B$ (respectivement à trois états $A$, $B$ et $C$) si :
pour tout entier naturel $n$ et tout $x\in \lbrace A;B\rbrace$ (respectivement $x\in \lbrace A;B;C\rbrace$) alors $p(X_{n+1}=x)$ ne dépend que de l'état à l'étape $n$.
La distribution initiale est la loi de probabilité pour $n=0$.Si on note A et B les sommets du graphe, 30% de ceux qui ont pris le minibus la veille choisissent la bicyclette se traduit par 30% passent de A vers BLe temps du jours suivant ne dépend que du temps constaté le jours précédent
donc on peut modéliser cette situation avec une chaîne de Markov à trois états $E_n=\begin{bmatrix}V_n&N_n&G_n\end{bmatrix}$ où $V_n$ est la probabilité qu'il vente après $n$ jours, $N_n$ est la probabilité qu'il vente après $n$ jours, $G_n$ est la probabilité qu'il vente après $n$ jours.
On a donc $V_n+N_n+G_n=1$
Le vent et la grêle ne restent jamais deux jours de suite.
donc $p_{V_n}(V_{n+1})=p_{G_n}(G_{n+1})=0$
S'il vente un jours donné, le lendemain il neige ou il grêle de manière équiprobable
donc $p_{V_n}(N_{n+1})=p_{V_n}(G_{n+1})=0,5$
S'il neige un jours donné, il y a une chance sur 3 qu'il vente le lendemain et une chance sur deux qu'il continue à neiger le lendemain
donc $p_{N_n}(V_{n+1})=\dfrac{1}{3}$ et $p_{N_n}(N_{n+1})=0,5$
Après un jour de grêle il y a deux fois plus de chance d'avoir de la neige que du vent
donc $p_{G_n}(N_{n+1})=\dfrac{2}{3}$ et $p_{G_n}(V_{n+1})=\dfrac{1}{3}$
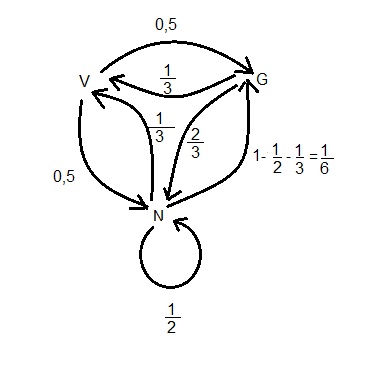
- Donner la matrice de transition, notée , associée à cette chaîne de Markov.
Matrice de transition d'un graphe probabiliste
La matrice de transition d'une chaîne de Markov à $n$ états est une matrice carrée $M=(m_{ij})$ d'ordre $n$ telle que $m_{ij}$ est le poids de l'arête allant du sommet $S_i$ au sommet $S_j$.
e coefficient de la ligne 1 et de la colonne 1 correspond à la probabilité de A sachant que A est réalisé la veille.Avec les sommets classés dans l'ordre $V$, $N$ et $G$ puisque l'on a choisit $E=\begin{bmatrix}V_n&N_n&G_n\end{bmatrix}$:
$T=\begin{bmatrix} 0&0,5&0,5\\ \dfrac{1}{3}&0,5&\dfrac{1}{6}\\ \dfrac{1}{3}&\dfrac{2}{3}&0 \end{bmatrix}$
La somme des coefficients de chaque ligne doit être égale à 1. - Quel est le temps le plus probable après un jour de Grêle?
On peut utiliser alors l'état initial $E_0=\begin{bmatrix}0&0&1\end{bmatrix}S'il y a un jour de grêle on peut utiliser l'état initial $E_0=\begin{bmatrix}0&0&1\end{bmatrix}$
$E_{1} =E_0\times T$
$~~~~=\begin{bmatrix}0&0&1\end{bmatrix}\times \begin{bmatrix} 0&0,5&0,5\\ \dfrac{1}{3}&0,5&\dfrac{1}{6}\\ \dfrac{1}{3}&\dfrac{2}{3}&0 \end{bmatrix}$
$~~~~=\begin{bmatrix}\dfrac{1}{3}&\dfrac{2}{3}&0\end{bmatrix}$
- Quel est la probabilité qu'après deux jours de neige, le vent tombe le lendemain?
l'état suivant ne dépend que du précédent
On peut utiliser alors l'état initial $E_0=\begin{bmatrix}0&1&0\end{bmatrix}L'état suivant ne dépend que du précédent donc on peut utiliser l'état initial $E_0=\begin{bmatrix}0&1&0\end{bmatrix}$
$E_{1} =E_0\times T$
$~~~~=\begin{bmatrix}0&1&0\end{bmatrix}\times \begin{bmatrix} 0&0,5&0,5\\ \dfrac{1}{3}&0,5&\dfrac{1}{6}\\ \dfrac{1}{3}&\dfrac{2}{3}&0 \end{bmatrix}$
$~~~~=\begin{bmatrix}\dfrac{1}{3}&0,5&\dfrac{1}{6}\end{bmatrix}$
donc $p_{N_{n}}(\overline{V_{n+1}})=1-\dfrac{1}{3}=\dfrac{2}{3}$
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
