Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
Pendant ses vacances d'été, Alex a la possibilité d'aller se baigner tous les jours. S'il va se baigner un jour, la probabilité qu'il aille se baigner le lendemain est de $0,7$.
S'il ne va pas se baigner un jour, la probabilité qu'il aille se baigner le lendemain est de $0,9$.
Le premier jour de ses vacances, Alex va se baigner.
$n$ étant un entier naturel non nul, on note :
$a_{n}$ la probabilité qu'Alex n'aille pas se baigner le $n$-ième jour.
$b_{n}$ la probabilité qu'Alex aille se baigner le $n$-ième jour.
$P_{n} = \begin{pmatrix} a_n&b_n \end{pmatrix}$ la matrice ligne traduisant l'état probabiliste le $n$-ième jour.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
S'il ne va pas se baigner un jour, la probabilité qu'il aille se baigner le lendemain est de $0,9$.
Le premier jour de ses vacances, Alex va se baigner.
$n$ étant un entier naturel non nul, on note :
$a_{n}$ la probabilité qu'Alex n'aille pas se baigner le $n$-ième jour.
$b_{n}$ la probabilité qu'Alex aille se baigner le $n$-ième jour.
$P_{n} = \begin{pmatrix} a_n&b_n \end{pmatrix}$ la matrice ligne traduisant l'état probabiliste le $n$-ième jour.
- Représenter la situation par un graphe probabiliste de sommets A et B (B représentant l'état " Alex va se baigner ").
S'il va se baigner un jour, la probabilité qu'il aille se baigner le lendemain est de $0,7$, c'est à dire de passer de l'état B à l'état BS'il va se baigner un jour, la probabilité qu'il aille se baigner le lendemain est de $0,7$, c'est à dire de passer de l'état B à l'état B.
S'il ne va pas se baigner un jour, la probabilité qu'il aille se baigner le lendemain est de $0,9$, c'est à dire de passer de l'état A à l'état B.
On a donc:
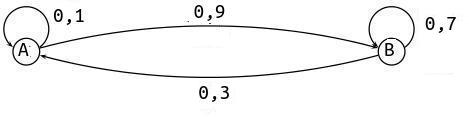
- Donner la matrice $M$ de transition associée à ce graphe et l'état initial.
Matrice de transition d'un graphe probabiliste
La matrice de transition d'une chaîne de Markov à $n$ états est une matrice carrée $M=(m_{ij})$ d'ordre $n$ telle que $m_{ij}$ est le poids de l'arête allant du sommet $S_i$ au sommet $S_j$.Le coefficient de la première ligne et de la deuxième colonne est la probabilité de passer de l'état A à l'état BLe coefficient de la première ligne et de la deuxième colonne est la probabilité de passer de l'état A à l'état B
Le coefficient de la deuxième ligne et de la première colonne est la probabilité de passer de l'état B à l'état A.
$M = \begin{pmatrix} 0,1& 0.9\\ 0,3 & 0,7\\ \end{pmatrix}$
Le premier jour de ses vacances, Alex va se baigner.
La somme des coefficients de chaque ligne doit être égale à 1. - Montrer que pour tout entier $n$ non nul, $b_{n+1} = 0,9a_{n} + 0,7 b_{n}$.
Calculer $P_{n}\times M$ et on a $E_{n+1}=\begin{pmatrix}a_{n+1}&b_{n+1} \end{pmatrix}$Pour tout entier naturel $n$, on a $E_{n+1}=E_n\times M$
$E_n\times M=\begin{pmatrix} a_n&b_n \end{pmatrix}\times \begin{pmatrix} 0,1& 0.9\\ 0,3 & 0,7\\ \end{pmatrix}=\begin{pmatrix} 0,1a_n+0,3b_n&0,9a_n+0,7b_n \end{pmatrix}$
$E_{n+1}=E_n\times M \Longleftrightarrow \begin{pmatrix} a_{n+1}&b_{n+1} \end{pmatrix}=\begin{pmatrix} 0,1a_n+0,3b_n&0,9a_n+0,7b_n \end{pmatrix}$
$\phantom{E_{n+1}=E_n\times M} \Longleftrightarrow \begin{cases} a_{n+1}=0,1a_n+0,3b_n\\ b_{n+1}=0,9a_n+0,7b_n \end{cases}$
- En déduire que : $b_{n+1} = - 0,2b_{n} + 0,9$.
On a $a_n+b_n=1$ donc $a_n=1-b_n$ que l'on peut remplacer dans l'égalité de la question précédente.Pour tout entier naturel $n$, on a $a_n+b_n=1$ soit $a_n=1-b_n$.
En utilisant la question précédente et en remplaçant $a_n$ par $1-b_n$, on a:
$b_{n+1}=0,9a_n+0,7b_n$
$\phantom{b_{n+1}}=0,9(1-b_n)+0,7b_n$
$\phantom{b_{n+1}}=0,9-0,9b_n+0,7b_n$
$\phantom{b_{n+1}}=-0,2b_n+0,9$
- On considère la suite $(u_n)$ définie pour tout entier $n$ non nul par $u_{n} = b_{n} - 0,75$.
Montrer que $(u_n)$ est une suite géométrique de raison $- 0,2$ ; on précisera son premier terme.Suite géométrique
Une suite $(u_n)$ est géométrique s'il existe un réel $q$ tel que pour tout entier naturel $n$, $u_{n+1}=u_n\times q$
$q$ est la raison de la suite.
Le quotient de deux termes consécutifs est égal à la raison soit $\dfrac{u_{n+1}}{u_n}=q$Forme explicite d'une suite géométrique
Si $(u_n)$ est géométrique de raison $q$ est premier terme $u_0$, on a:
$u_n=u_0\times q^n$
et pour tous entiers $n$ et $p$, $u_n=u_p\times q^{n-p}$$u_{n+1}=b_{n+1}-0,75=-0,2b_n+0,9-0,75$...Pour tout entier naturel $n$, on a $u_n=b_n-0,75$ donc $u_{n+1}=b_{n+1}-0,75$
et on a aussi $b_{n+1}=-0,2b_n+0,9$
$u_{n+1}=b_{n+1}-0,75$
$\phantom{u_{n+1}}=-0,2b_n+0,9-0,75$
$\phantom{u_{n+1}}=-0,2b_n+0,15$
$\phantom{u_{n+1}}=-0,2(b_n-0,75)$ (on factorise par le coefficient de $b_n$ et $0,2\times 0,75=0,15$)
$\phantom{u_{n+1}}=-0,2u_n$
$E_1=\begin{pmatrix} a_1&b_1 \end{pmatrix}=\begin{pmatrix} 0& 1 \end{pmatrix}$ donc $b_1=1$
Pour $n=1$, on a $u_1=b_1-0,75=1-0,75=0,25$
- En déduire l'expression de $u_n$ puis de $b_n$ en fonction de $n$.
include('rappels_cours/1/exp_geo.php');Le premier terme de la suite $(u_n)$ est $u_1$fat
On a $u_n=b_n-0,75$ donc $b_n=u_n+0,75$$(u_n)$ est une suite géométrique de raison $q=-0,2$ et premier terme $u_1=0,25$ donc pour tout entier naturel $n$, on a:
$u_n=u_1\times q^{n-1}=0,25\times (-0,2)^{n-1}$
$u_n=b_n-0,75$ donc $b_n=u_n+0,75=0,25\times (-0,2)^{n-1}+0,75$
- Quelle est la probabilité qu'il aille se baigner le 5ième jour de ses vacances ?
- Déterminer la limite de la suite $(b_n)$.
Limite de $q^n$
$\displaystyle \lim_{n \rightarrow +\infty}q^n=0$ pour $-1< q < 1$
Si $q> 1 $ alors $\displaystyle \lim_{n \rightarrow +\infty}q^n=+\infty$La raison de la suite géométrique $(u_n)$ est $q=-0,2$ et $-1 < q <1$
donc $\displaystyle\lim_{n \to + \infty} u_{n}=0$.
$\displaystyle\lim_{n \to + \infty} u_{n}=0$ et $b_n=u_n+0,75$
On a alors $\displaystyle\lim_{n \to + \infty} a_{n}=1-0,75=0,25$
Ces deux limites correspondent aux valeurs de l'état stable $E=\begin{pmatrix} 0,25&0,75 \end{pmatrix}$ et on a $E\times M=E$ - Retrouver l'état stable en utilisant la matrice de transition.
État stable ou chaîne de Markov stationnaire
On dit qu'une distribution $E$, représentée à l'aide d'une matrice ligne, est stationnaire pour une chaîne de Markov dont la matrice de transition est $M$ si $E=E\times M$.On pose $E=\begin{bmatrix} a& b\end{bmatrix}$
$E=E\times M$
$E\times M=\begin{pmatrix} a&b \end{pmatrix}\times \begin{pmatrix} 0,1& 0.9\\ 0,3 & 0,7\\ \end{pmatrix}=\begin{pmatrix} 0,1a+0,3&0,9a+0,7b \end{pmatrix}$
$E=E\times M \Longleftrightarrow \begin{pmatrix} a&b \end{pmatrix}=\begin{pmatrix} 0,1a+0,3b&0,9a+0,7b \end{pmatrix}$
et $a+b=1$ donc il faut résoudre $\begin{cases}a=0,1a+0,3b&a+b=1\end{cases}$
$\begin{cases}a=0,1a+0,3b&a+b=1\end{cases}\Longleftrightarrow \begin{cases}-0,9a+0,3b=0&a=1-b\end{cases}$
$\phantom{\begin{cases}a=0,1a+0,3b&a+b=1\end{cases}}\Longleftrightarrow \begin{cases}-0,9(1-b)+0,3b=0&a=1-b\end{cases}$
$\phantom{\begin{cases}a=0,1a+0,3b&a+b=1\end{cases}}\Longleftrightarrow \begin{cases}-0,9+0,9b+0,3b=0&a=1-b\end{cases}$
$\phantom{\begin{cases}a=0,1a+0,3b&a+b=1\end{cases}}\Longleftrightarrow \begin{cases}1,2b=0,9&a=1-b\end{cases}$
$\phantom{\begin{cases}a=0,1a+0,3b&a+b=1\end{cases}}\Longleftrightarrow \begin{cases}b=\dfrac{0,9}{1,2}&a=1-b\end{cases}$
$\phantom{\begin{cases}a=0,1a+0,3b&a+b=1\end{cases}}\Longleftrightarrow \begin{cases}b=\dfrac{3}{4}&a=\dfrac{1}{4}\end{cases}$
On a donc $\displaystyle\lim_{n \to + \infty} a_{n}=a=0,25$ et $\displaystyle\lim_{n \to + \infty} b_{n}=a=0,75$
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
