Publications MATHS-LYCEE.FR

mémo+exercices corrigés+liens vidéos

L'essentiel pour réussir la première en spécialité maths

RÉUSSIR EN MATHS, C'EST POSSIBLE!
Tous les chapitres avec pour chaque notion:
- mémo cours
- exercices corrigés d'application directe
- liens vidéos d'explications.
Il est indispensable de maîtriser parfaitement les notions de base et leur application directe pour pourvoir ensuite les utiliser dans la résolution de problèmes plus complexes.

Plus d'infos
  1. spécialité maths terminale
  2. chapitre 12 Graphes et chaînes de Markov
  3. exercice corrigé nº1543

Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!

Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.
*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
PDF reservé aux abonnés
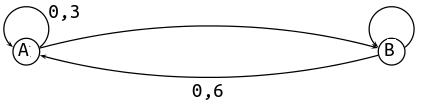
On donne le graphe probabiliste ci-dessous avec les événements A et B.
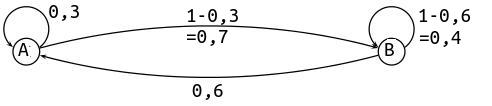
  1. Compléter le graphe avec les deux probabilités manquantes.

    Rappel de cours

    Graphe probabiliste

    Un graphe probabiliste est un graphe pondéré et la somme des coefficients des arêtes partant d'un sommet est égale à 1.

    Solution

    La somme des probabilités des branches partant d'un sommet est égale à 1.
  2. Ecrire la matrice $M$ de ce graphe probabiliste (les sommets étant classés par ordre alphabétique).

    Rappel de cours

    Matrice de transition d'un graphe probabiliste

    La matrice de transition d'une chaîne de Markov à $n$ états est une matrice carrée $M=(m_{ij})$ d'ordre $n$ telle que $m_{ij}$ est le poids de l'arête allant du sommet $S_i$ au sommet $S_j$.

    Aide

    Le coefficient de la ligne 1 et de la colonne 1 correspond à la probabilité de A sachant que A est réalisé à l'étape précédente.

    Solution

    Le coefficient de la ligne 1 et de la colonne 1 correspond à la probabilité de A sachant que A est réalisé à l'étape précédente....

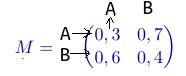
    $M=\begin{pmatrix} 0,3&0,7\\ 0,6&0,4 \end{pmatrix}$
    La somme des coefficients de chaque ligne doit être égale à 1.fat
  3. On note $E_n=\begin{pmatrix} a_n & b_n \end{pmatrix}$ la matrice après $n$ transitions et l'état initial est $E_0=\begin{pmatrix} 0,2&0,8 \end{pmatrix}$.
    Calculer $E_1$

    Aide

    On a $E_{n+1}=E_n\times M$

    Solution

    On a $M=\begin{pmatrix} 0,3&0,7\\ 0,6&0,4 \end{pmatrix}$
    $E_1=E_0\times M$

    $\phantom{E_1}=\begin{pmatrix} 0,2&0,8 \end{pmatrix}\times \begin{pmatrix} 0,3&0,7\\ 0,6&0,4 \end{pmatrix}$

    $\phantom{E_1}= \begin{pmatrix} 0,2\times 0,3+0,8\times 0,6 & 0,2\times 0,7+0,8\times 0,4 \end{pmatrix}$

    $\phantom{E_1}= \begin{pmatrix} 0,54 & 0,46 \end{pmatrix}$
  4. Exprimer $E_n$ en fonction de $E_0$ et de $n$.

    Aide

    $E_1=E_0\times M$, $E_2=E_1\times M=E_0\times M^2$

    Solution

    $E_1=E_0\times M$
    $E_2=E_1\times M=E_0\times M \times M=E_0\times M^2$ $E_3=E_2\times M=e_0\times M^3$
    .....$E_{n}=E_0\times M^n$
  5. Déterminer l'état stable $E=\begin{pmatrix} x& y \end{pmatrix}$

    Rappel de cours

    État stable ou chaîne de Markov stationnaire

    On dit qu'une distribution $E$, représentée à l'aide d'une matrice ligne, est stationnaire pour une chaîne de Markov dont la matrice de transition est $M$ si $E=E\times M$.

    Solution

    $E=E\times M$

    $\begin{pmatrix} x& y \end{pmatrix}\times \begin{pmatrix} 0,3&0,7\\ 0,6&0,4 \end{pmatrix}=\begin{pmatrix} 0,3x+0,6y&0,7x+0,4y \end{pmatrix}$
    On doit donc avoir $x=0,3x+0,6y$ et $y=0,7x+0,4y$
    On a de plus $x+y=1$.
    Il faut résoudre le système d'équations suivant par substitution:
    $\begin{cases} x+y=1\\ 0,3x+0,6y=x \end{cases}\Longleftrightarrow \begin{cases} y=1-x\\ 0,3x+0,6(1-x)=x \end{cases}$

    $\phantom{\begin{cases} x+y=1\\ 0,3x+0,6y=x \end{cases}}\Longleftrightarrow \begin{cases} y=1-x\\ 0,3x+0,6-0,6x=x \end{cases}$

    $\phantom{\begin{cases} x+y=1\\ 0,3x+0,6y=x \end{cases}}\Longleftrightarrow \begin{cases} y=1-x\\ 0,3x-0,6x-x=-0,6 \end{cases}$

    $\phantom{\begin{cases} x+y=1\\ 0,3x+0,6y=x \end{cases}}\Longleftrightarrow \begin{cases} y=1-x\\ -1,3x=-0,6 \end{cases}$

    $\phantom{\begin{cases} x+y=1\\ 0,3x+0,6y=x \end{cases}}\Longleftrightarrow \begin{cases} y=1-\dfrac{6}{13}\\ x=\dfrac{6}{13} \end{cases}$

    $\phantom{\begin{cases} x+y=1\\ 0,3x+0,6y=x \end{cases}}\Longleftrightarrow \begin{cases} y=\dfrac{7}{13}\\ x=\dfrac{6}{13} \end{cases}$


    Penser à contrôler le résultat avec la calculatrice en saisissant les matrices $M$ et $E$ et en calculant $E\times M$

Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)