La classe de Terminale d'Arthur est en voyage scolaire en Angleterre.
Les professeurs organisateurs de ce voyage décident de visiter plusieurs sites de Londres.
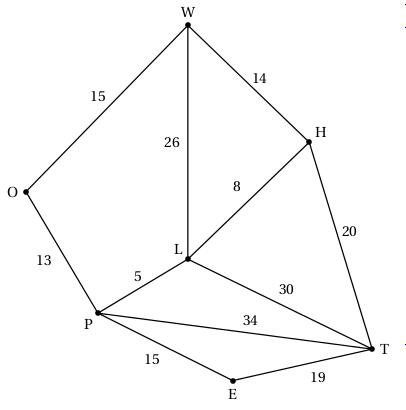
Les sites retenus dans Londres sont les suivants : Warren Street, Oxford Circus, Piccadilly Circus, Leicester Square, Holborn, Embankment et Temple. Ces lieux sont désignés respectivement par les lettres W, O, P, L, H, E et T et sont représentés dans le graphe $\Gamma$ donné ci-dessus (chaque sommet représente un site à visiter et chaque arête une route reliant deux sites).
Les élèves sont laissés en autonomie deux heures pour faire du shopping et ramener des souvenirs~à leurs familles. Le point de rendez-vous avec les organisateurs est fixé à Temple. Les temps de parcours en minutes entre chaque sommet ont été ajoutés sur le graphe.

Arthur, qui est à Oxford Circus, n'a pas vu le temps passer. Lorsqu'il s'en rend compte, il ne lui reste plus que 40~minutes pour arriver à Temple.

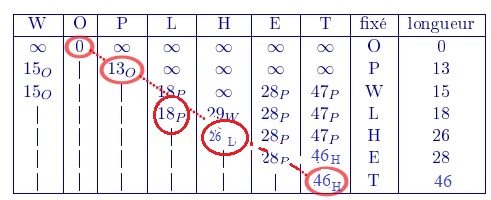
1. Déterminer le plus court chemin en minutes reliant Oxford Circus à Temple. Justifier la réponse à l'aide d'un algorithme.

   Aide

   On part du sommet O pour aller au sommet T.
   On a donc dans la première étape $15_O$ pour le sommet W et $13_O$ pour le sommet P.

   Solution

   On utilise l'algorithme de Dijkstra.
   
   Le plus court chemin pour aller de O à T est OPLHT. Remarque
   On peut aussi faire le trajet $OPT$ qui donne le même temps.
2. Quelle est la longueur en minutes de ce chemin ? Arthur sera-t-il en retard ?

   Aide

   Le plus court chemin pour aller de O à T doit prendre moins de 40 mn.

   Solution

   La longueur, en minutes, du plus court chemin est de 46mn soit plus de 40 mn donc Arthur ne pourra pas arriver à temps.
   Arthur sera en retard.