Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
Un orchestre doit effectuer une tournée passant par les villes A, B, C, D, E, F, G et H, en utilisant le réseau autoroutier.
Des contraintes de calendrier imposent en fait d'organiser un concert dans la ville F immédiatement après un concert dans la ville A.
Le graphe $\Gamma$ ci-dessous représente les différentes villes de la tournée et les autoroutes reliant ces villes (une ville est représentée par un point, une autoroute par une arête).
Le graphe $\Gamma$ est complété par les longueurs en kilomètres de chaque tronçon (les longueurs des segments ne sont pas proportionnelles aux distances).
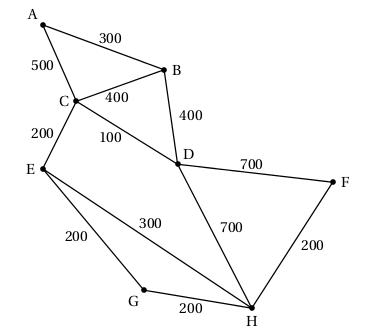
Déterminer, en utilisant un algorithme dont on citera le nom, le trajet autoroutier le plus court (en kilomètres) pour aller de A à F.
Préciser la longueur en kilomètres de ce trajet.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Des contraintes de calendrier imposent en fait d'organiser un concert dans la ville F immédiatement après un concert dans la ville A.
Le graphe $\Gamma$ ci-dessous représente les différentes villes de la tournée et les autoroutes reliant ces villes (une ville est représentée par un point, une autoroute par une arête).
Le graphe $\Gamma$ est complété par les longueurs en kilomètres de chaque tronçon (les longueurs des segments ne sont pas proportionnelles aux distances).

Déterminer, en utilisant un algorithme dont on citera le nom, le trajet autoroutier le plus court (en kilomètres) pour aller de A à F.
Préciser la longueur en kilomètres de ce trajet.
Le tableau commence comme indiqué ci-dessous:
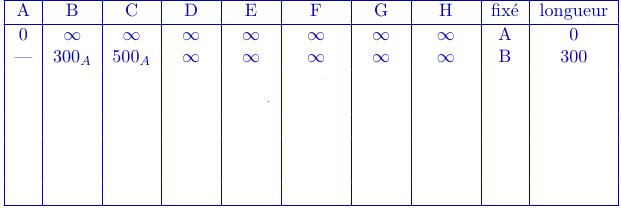

On utilise l'algorithme de Dijkstra.
Le départ a lieu au sommet A.
Le sommet A est adjacent aux sommets B et C.
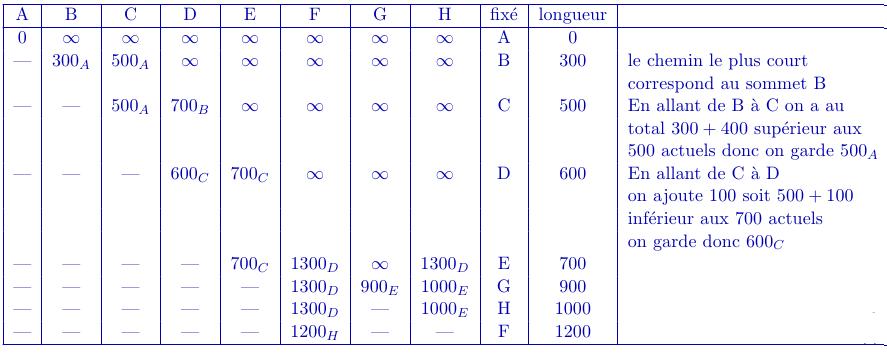
On utilise les sommets notés avec les longueurs dans le tableau(voir figure ci-dessous):
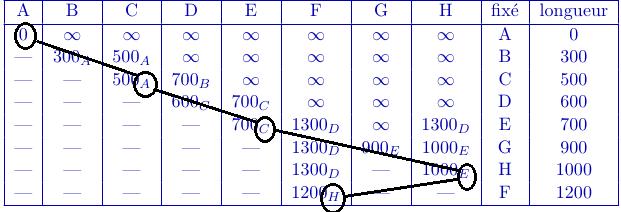
Le départ a lieu au sommet A.
Le sommet A est adjacent aux sommets B et C.

On utilise les sommets notés avec les longueurs dans le tableau(voir figure ci-dessous):

Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
