Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
On donne ci-dessous le graphe pondéré $G$ à 5 sommets.
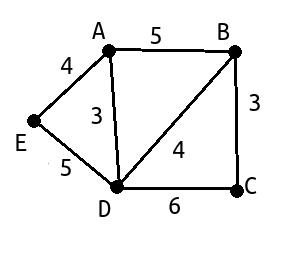
Déterminer le plus court chemin allant du sommet A au sommet C en utilisant l'algorithme de Dijkstra.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)

Déterminer le plus court chemin allant du sommet A au sommet C en utilisant l'algorithme de Dijkstra.
Etape 1: départ au sommet A
Le sommet A est adjacent aux sommets B, D et E.
On complète la ligne en provenance de A en indiquant le coefficient correspondant sur le graphe.
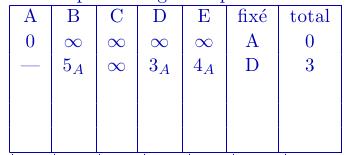
On sélectionne le plus court chemin, ici cela correspond au sommet D.
On repart du point D et ajoutant 3 aux coefficients.
Etape 2: en partant de D.
D est adjacent aux sommets B,C et E.
Par exemple, pour aller de D à B, on aura au total $3+4=7$ or pour le moment, il y a $5_A$, ce qui est inférieur à 7 donc on garde $5_A$.
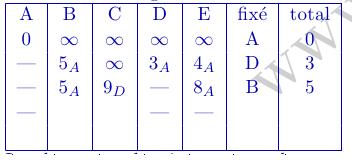
Le plus court chemin correspond au sommet B donc on repart cette fois du sommet B:
Etape 3: Départ de B
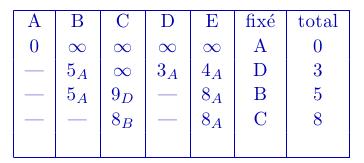
On indique avec chaque coefficient le sommet précédent pour déterminer ensuite le parcours le plus court (voir graphique ci-dessous)
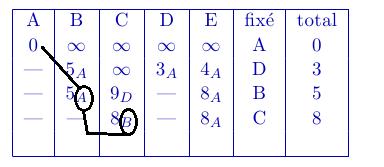
Le sommet A est adjacent aux sommets B, D et E.
On complète la ligne en provenance de A en indiquant le coefficient correspondant sur le graphe.

On sélectionne le plus court chemin, ici cela correspond au sommet D.
On repart du point D et ajoutant 3 aux coefficients.
Etape 2: en partant de D.
D est adjacent aux sommets B,C et E.
Par exemple, pour aller de D à B, on aura au total $3+4=7$ or pour le moment, il y a $5_A$, ce qui est inférieur à 7 donc on garde $5_A$.

Le plus court chemin correspond au sommet B donc on repart cette fois du sommet B:
Etape 3: Départ de B

On indique avec chaque coefficient le sommet précédent pour déterminer ensuite le parcours le plus court (voir graphique ci-dessous)

Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
