Publications MATHS-LYCEE.FR
Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
Dans chaque cas, écrire la matrice du graphe en ordonnant les sommets dans l'ordre alphabétique.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
- .
Matrice associée à un graphe
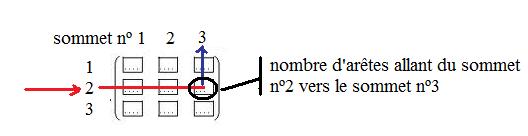
La matrice associée à un graphe d'ordre $n$ dont les sommets sont numérotés de 1 à n est une matrice carrée de dimension $n$, où le terme à l'intersection de la iième ligne et de la jième colonne est nombre d'arêtes reliant i et j.
Cette matrice est appelée matrice d'adjacence du graphe.
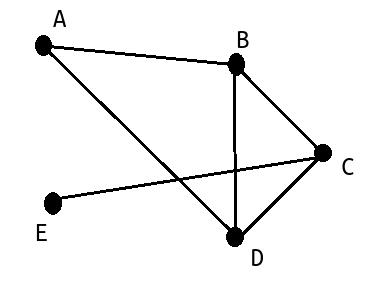
Il ya 5 sommets donc la matrice est une matrice carrée d'ordre 5
Les coefficients de la première ligne correspondent aux arêtes paratant du sommet ALe sommet de la ligne 1 est le sommet A
Par exemple, il y a une arête reliant du sommet A au sommet B (voir figure ci-dessous)
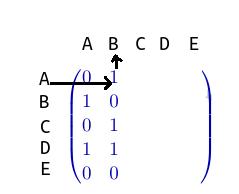
On peut contrôler les résultats en vérifiant que la somme des coefficients de chaque ligne est égale au degré du sommet correspondant à cette ligne.
La matrice obtenue est une matrice carrée symétrique dont les termes de la diagonale sont nuls. - .
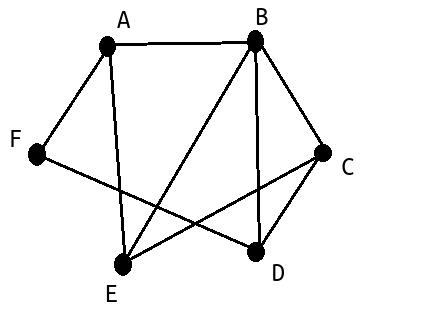
On peut vérifier que la matrice est bien symétrique (la diagonale est un axe de symétrie)
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)