Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
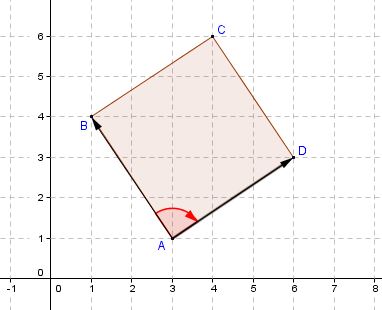
On donne les points $A$, $B$, $C$ et $D$ d'affixe respective $z_A=3+i$, $z_B=1+4i$, $z_C=4+6i$ et $z_D=6+3i$ dans un repère orthonormé $(O;\overrightarrow{i};\overrightarrow{j})$.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
- Calculer l'affixe des vecteurs $\overrightarrow{AB}$, $\overrightarrow{DC}$ et $\overrightarrow{AD}$.
Affixe d'un point et d'un vecteur
Le complexe $z=x+iy$ ($x$ et $y$ réels) est l'affixe du point $M(x;y)$. l Avec $\overrightarrow{u}(a;b)$, le complexe $u=a+ib$ est l'affixe du vecteur $\overrightarrow{u}$.$z_{\overrightarrow{AB}}=z_B-z_A=1+4i-(3+i)=-2+3i$
$z_{\overrightarrow{DC}}=z_C-z_D=4+6i-(6+3i)=4+6i-6-3i=-2+3i$
$z_{\overrightarrow{AD}}=z_D-z_A=6+3i-(3+i)=6+3i-3-i=3+2i$ - Calculer $AB$ et $AD$
Forme trigonométrique
Soit $z=x+iY$ un complexe.
Le module de $z$ noté $|z|$ est $|z|=OM=\sqrt{x^2+y^2}$.
Si $z\neq 0$ l'argument de $z$ noté $arg(z)$ est une mesure en radians de l'angle $(\overrightarrow{i};\overrightarrow{OM})$}
On a alors $x=|z|cos(arg(z))$ et $y=|z|sin(arg(z))$ soit $z=|z|(cos(arg(z)+isin(arg(z))$
Cette forme est appelée forme trigonométrique} de $z$.Il faut calculer $|z_B-z_A|$ et $|z_D-z_A|$.$AB=|z_B-z_A|=\sqrt{(-2)^2+3^2}=\sqrt{13}$
$AD=|z_D-z_A|=\sqrt{3^2+2^2}=\sqrt{13}$
- Donner la forme algébrique puis trigonométrique de $\dfrac{z_D-z_A}{z_B-z_A}$.
Équation réduite de deux droites parallèles
Dans un repère du plan, deux droites (non parallèles à l'axe des ordonnées) sont parallèles si et seulement si elles ont le même coefficient directeurIl faut multiplier le numérateur et le dénominateur par le conjugé du dénominateur$\dfrac{z_D-z_A}{z_B-z_A}=\dfrac{3+2i}{-2+3i}$
$\phantom{\dfrac{z_D-z_A}{z_B-z_A}}=\dfrac{(3+2i)(-2-3i)}{(-2+3i)(-2-3i)}$
$\phantom{\dfrac{z_D-z_A}{z_B-z_A}}=\dfrac{-6-9i-4i-6i^2}{(-2)^2+)(-3)^2}$
$\phantom{\dfrac{z_D-z_A}{z_B-z_A}}=\dfrac{-6-13i+6}{13}$
$\phantom{\dfrac{z_D-z_A}{z_B-z_A}}=\dfrac{-13i}{13}$
$\phantom{\dfrac{z_D-z_A}{z_B-z_A}}=-i$
- En déduire la nature du quadrilatère $ABCD$.
Angles et argument d'un quotient
Soient $A$ , $B$ et $C$ quatre points distincts d'affixes respectives $z_A$, $z_B$ et $z_C$.
$(\overrightarrow{AB},\overrightarrow{AC})=arg\left(\dfrac{z_C-z_A}{z_B-z_A}\right)$On a $z_B-z_A=z_D-z_A$ et $|z_B-z_A|=|z_D-z_A|$ puis l'argument de $-i$$AB=AD$ et $z_{\overrightarrow{AB}}=z_{\overrightarrow{DC}}=-2+3i$
donc $\overrightarrow{AB}=\overrightarrow{DC}$
On a aussi $arg(-i)=\dfrac{-\pi}{2}$ ($2\pi$)
donc $(\overrightarrow{AB};\overrightarrow{AD})=arg\left(\dfrac{z_D-z_A}{z_B-z_A}\right)=arg(-i)=-\dfrac{\pi}{2}$ ($2\pi$)
donc les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AD}$ sont orthogonaux
On a $\overrightarrow{AB}(-2;3)$ et $\overrightarrow{AD}(3;2)$.
$\overrightarrow{AB}.\overrightarrow{AD}=-2\times 3+3\times 2=0$
Le produit scalaire des deux vecteurs est nul donc ils sont orthogonaux.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
vidéos semblables
Pour compléter cet exercice, nous vous conseillons les vidéos suivantes semblables à l'exercice affiché.
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
