Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
On pose $P(z)=z^3+iz^2-iz+1+i$ défini pour $z\in \mathbb{C}$.
- Calculer $P(-1-i)$
On peut écrire $(-1-i)^3=(-1-i)^2(-1-i)$ pour développer $z^3$.$(-1-i)^2=(-1)^2+2\times (-1)\times (-i)+(-i)^2=1+2i-1=2i$
$(-1-i)^3=(-1-i)^2(-1-i)$
$\phantom{(-1-i)^3}=2i(-1-i)=-2i-2i^2=2-2i$
$P(-1-i)=(-1-i)^3+i(-1-i)^2-i(-1-i)+1+i$
$\phantom{P(-1-i)}=2-2i+i\times 2i+i+i^2+1+i$
$\phantom{P(-1-i)}=2-2i-2+i-1+1+i$
$\phantom{P(-1-i)}=3-3-2i+2i$
$\phantom{P(-1-i)}=0$
- On peut donc factoriser $P(z)$ par $z-(-1-i)=z+1+i$.
Déterminer $a$, $b$ et $c$ tels que $P(z)=(z+1+i)(az^2+bz+c)$ pour tout complexe $z$.Il faut développer l'expression $(z+1+i)(az^2+bz+c)$ et identifier les coefficients de $z^3$, de $z^2$, $z$ et la constante.$P(z)=(z+1+i)(az^2+bz+c)$
$\phantom{P(z)}=az^3+bz^2+cz+az^2+bz+c+aiz^2+biz+ci$
$\phantom{P(z)}=az^3+bz^2+az^2+aiz^2+bz+cz+biz+c+ci$
$\phantom{P(z)}=az^3+(b+a+ai)z^2+(b+c+bi)z+c+ci$ et on a $P(z)=z^3+iz^2-iz+1+i$ donc par identification des coefficients on a:
$\begin{cases} a=1\\ b+a+i=i\\ b+c+bi=-i\\ c+ci=1+i \end{cases}\Longleftrightarrow \begin{cases} a=1\\ b=-a=-1\\ -1+c-i=-i\\ c(1+i)=1+i \end{cases} \Longleftrightarrow \begin{cases} a=1\\ b=-a=-1\\ c=1\\ c=1 \end{cases}$
- En déduire les solutions de $P(z)=0$.
Équations du second degré à coefficients réels
équation du second degré à coefficients réels
Discriminant: $\Delta=b^2-4ac$
- Si $\Delta \geq 0$, on résout dans $\mathbb{R}$
Si $\Delta >0 $ il y a 2 racines $z_1=\dfrac{-b-\sqrt{\Delta}}{2a}$ et $z_2=\dfrac{-b+\sqrt{\Delta}}{2a}$
Si $\Delta <0$ alors on a deux racines complexes conjuguées:
$z_1=\dfrac{-b-i\sqrt{|\Delta|}}{2a}$ et $z_2=\dfrac{-b+i\sqrt{|\Delta|}}{2a}=\overline{z_1}$
Il faut utiliser la forme factorisée de $P(z)$ obtenue à la question 2 et un produit de facteurs nul.$P(z)=0 \Longleftrightarrow (z+1+i)(z^2-z+1)=0\Longleftrightarrow z+1+i=0$ ou $z^2-z+1=0$
$z+1+i=0 \Longleftrightarrow z=-1-i$
Résolution de $z^2-z+1=0$
$\Delta=b^2-4ac=(-1)^2-4\times 1\times 1=1-4=-3$
$z_1=\dfrac{-b+i\sqrt{|\Delta|}}{2a}=\dfrac{ 1+i\sqrt{3} }{2 }$
et $z_2=\dfrac{-b-i\sqrt{|\Delta|}}{2a}= \dfrac{1-i\sqrt{3} }{2 }$
donc $P(z)=0$ admet trois solutions dans $\mathbb{Z}$.
Penser à contrôler avec la calculatrice MENU équations puis saisir les coefficients. Penser à passer en mode complexe (casio: SHIFT SETUP puis COMPLEXE MODE)
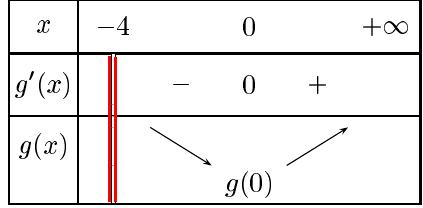
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)vidéos semblables
Pour compléter cet exercice, nous vous conseillons les vidéos suivantes semblables à l'exercice affiché.exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
