Publications MATHS-LYCEE.FR
Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
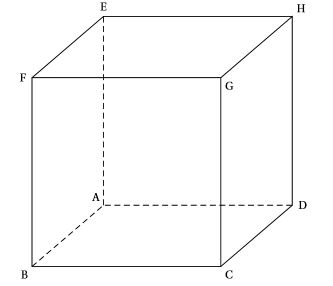
On considère un cube ABCDEFGH d'arête de longueur 1.
On se place dans le repère orthonormal $\left(\text{A};\overrightarrow{\text{AB}};\overrightarrow{\text{AD}};\overrightarrow{\text{AE}}\right)$.
On considère les points $I\left(1;\dfrac{1}{3};0\right)$, $J\left(0;\dfrac{2}{3};1\right)$, $K\left(\dfrac{3}{4};0;1\right)$ et $L(a;1;0)$ avec $a$ un nombre réel appartenant à l'intervalle [0;1].
Les parties A et B sont indépendantes.
Partie A
Partie B
Dans la suite de l'exercice, on pose $a = \frac{1}{4}$.
Le point L a donc pour coordonnées $\left(\frac{1}{4};1;0\right)$.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
On se place dans le repère orthonormal $\left(\text{A};\overrightarrow{\text{AB}};\overrightarrow{\text{AD}};\overrightarrow{\text{AE}}\right)$.
On considère les points $I\left(1;\dfrac{1}{3};0\right)$, $J\left(0;\dfrac{2}{3};1\right)$, $K\left(\dfrac{3}{4};0;1\right)$ et $L(a;1;0)$ avec $a$ un nombre réel appartenant à l'intervalle [0;1].
Les parties A et B sont indépendantes.
Partie A
- Déterminer une représentation paramétrique de la droite $(IJ)$.
Vecteur normal à un plan-équation cartésienne d'un plan
Dans l'espace muni d'un repère othonormé, $P$ est un plan de l'espace, un vecteur $\overrightarrow{n}$ normal à $P$ est un vecteur directeur d'une droite orthogonale à $P$.
Le vecteur $\overrightarrow{n}$ est un vecteur normal au plan $P$ passant par $A$ et $P$ est l'ensemble des points $M(x;y;z)$ vérifiant $\overrightarrow{AM}.\overrightarrow{n}=0$.
$ax+by+cz+d=0$ est une équation cartésienne de $P$ de vecteur normal $\overrightarrow{n}\begin{pmatrix} a\\ b\\ c \end{pmatrix}$$\overrightarrow{IJ}$ est un vecteur directeur de $(IJ)$$\overrightarrow{IJ}$ est un vecteur directeur de la droite $(IJ)$.
$\begin{cases} x_{\overrightarrow{IJ}}=x_J-x_I=0-1=-1\\ y_{\overrightarrow{IJ}}=y_J-y_I=\dfrac{2}{3}-\dfrac{1}{3}=\dfrac{1}{3}\\ z_{\overrightarrow{IJ}}=z_J-z_I=1-0=1 \end{cases}$
donc $\overrightarrow{IJ}\begin{pmatrix} -1\\ \dfrac{1}{3}\\ 1 \end{pmatrix} $
Si $M(x;y;z)$ un point de $(IJ)$,on a alors:
$\begin{cases} x=x_I+tx_{\overrightarrow{IJ}}=1-t\\ y=y_I+ty_{\overrightarrow{IJ}}=\dfrac{1}{3}+t\times \dfrac{1}{3}\\ z=z_I+tz_{\overrightarrow{IJ}}=0+t\\ \end{cases}$
- Donner de même une représentation paramétrique de la droite $(KL)$.
$\overrightarrow{KL}\begin{pmatrix} a-\dfrac{3}{4}\\ 1\\ -1 \end{pmatrix}$
donc si $M(x;y;z)$ appartient à $(IK)$ on a $\begin{cases} x=x_K+t'x_{\overrightarrow{KL}}=\dfrac{3}{4}+t'\times \left(a-\dfrac{3}{4}\right)\\ y=y_K+t'y_{\overrightarrow{KL}}=0+t'\\ z=z_K+t'z_{\overrightarrow{KL}}=1-t'\\ \end{cases}$
- Démontrer que les droites $(IJ)$ et $(KL)$ sont sécantes si, et seulement si $a=\dfrac{1}{4}$.
Si on note $U$ le point d'intersection s'il existe des droites $(IJ)$ et $(KL)$ il existe un réel $t$ et un réel $t'$ tel que $y_U=\dfrac{1+t}{3}=t'$ et $z_U=t=1-t'$
Avec les valeurs de $t$ et $t'$ obtenues ont peut écrire une équation d'inconnue $a$ en utilisant les abscisses.Si le point d'intersection de $(IJ)$ et $KL)$ existe alors il existe un couple de réel $(t;t')$ tel que:
$\begin{cases} x=1-t=\dfrac{3}{4}+t'\times \left(a-\dfrac{3}{4}\right)\\ y=\dfrac{1+t}{3}=t'\\ z=t=1-t' \end{cases}$
On peut déterminer $t$ et $t'$ en utilisant les deux dernières équations:
$\begin{cases} \dfrac{1+t}{3}=t'\\ t=1-t' \end{cases}\Longleftrightarrow \begin{cases} 1+t=3t'\\ t=1-t' \end{cases}$
$\phantom{\begin{cases} \dfrac{1+t}{3}=t'\\ t=1-t' \end{cases}}\Longleftrightarrow \begin{cases} 1+1-t'=3t'\\ t=1-t' \end{cases}$
$\phantom{\begin{cases} \dfrac{1+t}{3}=t'\\ t=1-t' \end{cases}}\Longleftrightarrow \begin{cases} -4t'=-2\\ t=1-t' \end{cases}$
$\phantom{\begin{cases} \dfrac{1+t}{3}=t'\\ t=1-t' \end{cases}}\Longleftrightarrow \begin{cases} t'=\dfrac{1}{2}\\ t=1-\dfrac{1}{2} \end{cases}$
$\phantom{\begin{cases} \dfrac{1+t}{3}=t'\\ t=1-t' \end{cases}}\Longleftrightarrow \begin{cases} t'=\dfrac{1}{2}\\ t=\dfrac{1}{2} \end{cases}$
En remplaçant $t$ et $t'$ par ces valeurs dans la première équation, on obtient:
$1-\dfrac{1}{2}=\dfrac{3}{4}+\dfrac{1}{2}\times \left(a-\dfrac{3}{4}\right)$
$ \Longleftrightarrow \dfrac{1}{2}=\dfrac{3}{4}+\dfrac{a}{2}-\dfrac{3}{8}$
$ \Longleftrightarrow 4=6+4a-3$ (on multiplie les deux membres par 8 pour se "débarrasser" des fractions
$ \Longleftrightarrow -4a=-1$
$ \Longleftrightarrow a=\dfrac{1}{4}$
En remplaçant $t$ par $\dfrac{1}{2}$ dans la représentation paramétrique de $(IJ)$ on obtient les coordonnées du point d'intersection des deux droites
Partie B
Dans la suite de l'exercice, on pose $a = \frac{1}{4}$.
Le point L a donc pour coordonnées $\left(\frac{1}{4};1;0\right)$.
- Démontrer que le quadrilatère $IKJL$ est un parallélogramme.
Coordonnées d'un vecteur dans l'espace
L'espace est muni d'un repère quelconque.
Soit $A(x_A;y_A;z_A)$ et $B(x_B;y_B;z_B)$
$\overrightarrow{AB}\begin{pmatrix} x_B-x_A\\ y_B-y_A\\ z_B-z_A \end{pmatrix} $$IKJL$ est un parallélogramme $\Longleftrightarrow \overrightarrow{IK}=\overrightarrow{LJ}$$\overrightarrow{IK}\begin{pmatrix} -\dfrac{1}{4}\\ -\dfrac{1}{3}\\ 1 \end{pmatrix} $
et $\overrightarrow{LJ}\begin{pmatrix} -\dfrac{1}{4}\\ -\dfrac{1}{3}\\ 1 \end{pmatrix}$
donc $\overrightarrow{IK}=\overrightarrow{LJ}$
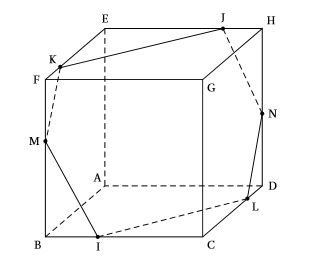
- La figure ci-dessous fait apparaître l'intersection du plan $(IJK)$ avec les faces du cube $ABCDEFGH$ telle qu'elle a été obtenue à l'aide d'un logiciel de géométrie dynamique.
On désigne par $M$ le point d'intersection du plan $(IJK)$ et de la droite $(BF)$ et par $N$ le point d'intersection du plan $(IJK)$ et de la droite $(DH)$.
Le but de cette question est de déterminer les coordonnées des points M et N.- Prouver que le vecteur $\overrightarrow{n}\begin{pmatrix}
8\\
9\\
5
\end{pmatrix}$
est un vecteur normal au plan $(IJK)$.
droite et plan orthogonaux
Une droite $(d)$ est orthogonale à un plan si et seulement si un vecteur directeur de $(d)$ est orthogonal à deux vecteurs directeurs de du plan.
Il faut montrer que le vecteur $\overrightarrow{n}$ est orthogonal aux vecteurs directeurs $\overrightarrow{IJ}$ et $\overrightarrow{IK}$ du plan $(IJK)$$\overrightarrow{IJ}\begin{pmatrix} -1\\ \dfrac{1}{3}\\ 1 \end{pmatrix} $
et $\overrightarrow{IJ}.\overrightarrow{n}=-1\times 8+\dfrac{1}{3}\times 9+1\times 5=-8+3+5=0$
donc $\overrightarrow{IJ}$ et $\overrightarrow{n}$ sont orthogonaux.
$\overrightarrow{IK}\begin{pmatrix} -\dfrac{1}{4}\\ -\dfrac{1}{3}\\ 1 \end{pmatrix} $
et $\overrightarrow{IL}.\overrightarrow{n}=-\dfrac{1}{4}\times 8-\dfrac{1}{3}\times 9+1\times 5=-2-3+5=0$
donc $\overrightarrow{IK}$ et $\overrightarrow{n}$ sont orthogonaux.
le vecteur $\overrightarrow{n}$ est orthogonal aux vecteurs directeurs $\overrightarrow{IJ}$ et $\overrightarrow{IK}$ du plan $(IJK)$
- En déduire que le plan (IJK) a pour équation $8x+9y+5z-11=0$.
Vecteur normal à un plan-équation cartésienne d'un plan
Dans l'espace muni d'un repère othonormé, $P$ est un plan de l'espace, un vecteur $\overrightarrow{n}$ normal à $P$ est un vecteur directeur d'une droite orthogonale à $P$.
Le vecteur $\overrightarrow{n}$ est un vecteur normal au plan $P$ passant par $A$ et $P$ est l'ensemble des points $M(x;y;z)$ vérifiant $\overrightarrow{AM}.\overrightarrow{n}=0$.
$ax+by+cz+d=0$ est une équation cartésienne de $P$ de vecteur normal $\overrightarrow{n}\begin{pmatrix} a\\ b\\ c \end{pmatrix}$Il faut utiliser les coordonnées du vecteur $\overrightarrow{n}$ vecteur normal au plan $(IJK)$ et les coordonnées de $I$ par exemple pour calculer $d$$\overrightarrow{n}\begin{pmatrix} 8\\ 9\\ 5 \end{pmatrix}$ est un vecteur normal au plan $(IJK)$ donc un équation cartésienne de $(IJK)$ est de la forme $8x+9y+5z+d=0$
$I\left(1;\dfrac{1}{3};0\right)\in (IJK) \Longleftrightarrow 8x_I+9y_I+5z_I+d=0$
$\phantom{I\left(1;\dfrac{1}{3};0\right)\in (IJK)} \Longleftrightarrow 8+9\times \dfrac{1}{3}+0+d=0$
$\phantom{I\left(1;\dfrac{1}{3};0\right)\in (IJK)} \Longleftrightarrow 11+d=0$
$\phantom{I\left(1;\dfrac{1}{3};0\right)\in (IJK)} \Longleftrightarrow d=-11$
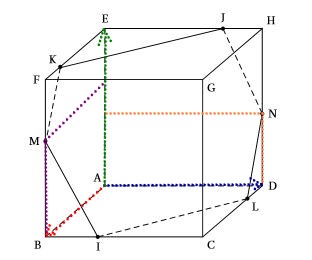
- En déduire les coordonnées des points $M$ et $N$.
Le point $M$ appartient au plan $(A;\overrightarrow{AB};\overrightarrow{AE})$ donc $y_M=0$
et le point $M$ appartient au plan $(BFG)$ donc $x_M=1$ et $M\in (IJK)$Le point $M$ appartient au plan $(A;\overrightarrow{AB};\overrightarrow{AE})$ donc $y_M=0$ et le point $M$ appartient au plan $(BFG)$ donc $x_M=1$
$M\in (IJK)\Longleftrightarrow 8x_M+9y_M+5z_M-11=0$
$M\in (IJK)\Longleftrightarrow 8+5z_M-11=0$
$\phantom{M\in (IJK)}\Longleftrightarrow 5z_M-3=0$
$\phantom{M\in (IJK)}\Longleftrightarrow z_M=\dfrac{3}{5}$
Le point $N$ appartient au plan $(A;\overrightarrow{AD};\overrightarrow{AE})$ donc $x_N=0$ et le point $N$ appartient au plan $(HDC)$ donc $y_N=1$
$N\in (IJK)\Longleftrightarrow 8x_N+9y_N+5z_N-11=0$
$\phantom{N\in (IJK)}\Longleftrightarrow 9+5z_N-11=0$
$\phantom{M\in (IJK)}\Longleftrightarrow 5z_N-2=0$
$\phantom{N\in (IJK)}\Longleftrightarrow z_N=\dfrac{2}{5}$
- Prouver que le vecteur $\overrightarrow{n}\begin{pmatrix}
8\\
9\\
5
\end{pmatrix}$
est un vecteur normal au plan $(IJK)$.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Fiche méthode
Si cet exercice vous pose problème, nous vous conseillons de consulter la fiche méthhode.
Equation cartésienne d'un plan
- vecteur normal
- déterminer une équation d'un plan
- position relative d'une droite et d'un plan
- intersection de droites et plans
infos: | 15-20mn |
vidéos semblables
Pour compléter cet exercice, nous vous conseillons les vidéos suivantes semblables à l'exercice affiché.
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.