Publications MATHS-LYCEE.FR

mémo+exercices corrigés+liens vidéos

L'essentiel pour réussir la première en spécialité maths

RÉUSSIR EN MATHS, C'EST POSSIBLE!
Tous les chapitres avec pour chaque notion:
- mémo cours
- exercices corrigés d'application directe
- liens vidéos d'explications.
Il est indispensable de maîtriser parfaitement les notions de base et leur application directe pour pourvoir ensuite les utiliser dans la résolution de problèmes plus complexes.

Plus d'infos
  1. spécialité maths terminale
  2. chapitre 8 Géométrie dans l'espace
  3. exercice corrigé nº1343

Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!

Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.
*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
PDF reservé aux abonnés
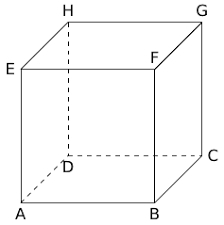
$ABCDEFGH$ est un cube de côté $a$.

  1. Calculer $\overrightarrow{FD}.\overrightarrow{EG}$.

    Rappel de cours

    relation de Chasles

    $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$

    Orthogonalité et produit scalaire

    Pour tous vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$, on a:
    $\overrightarrow{u}.\overrightarrow{v}=0 \Longleftrightarrow \overrightarrow{u}=\overrightarrow{0}$ ou $\overrightarrow{v}=\overrightarrow{0}$ ou $\overrightarrow{u}$ et $\overrightarrow{v}$ sont orthogonaux.

    Aide

    $\overrightarrow{FD}=\overrightarrow{FH}+\overrightarrow{HD}$ et $\overrightarrow{EG}=\overrightarrow{EF}+\overrightarrow{FG}$

    Solution

    $\overrightarrow{EG}.\overrightarrow{FD}$
    $=(\overrightarrow{EF}+\overrightarrow{FG}).(\overrightarrow{FH}+\overrightarrow{HD})$
    $=(\overrightarrow{EF}+\overrightarrow{FG}).(\overrightarrow{FH}+\overrightarrow{HD})$
    $=\overrightarrow{EF}.\overrightarrow{FH}+\overrightarrow{EF}.\overrightarrow{HD}+\overrightarrow{FG}.\overrightarrow{FH}+\overrightarrow{FG}.\overrightarrow{HD}$
    $=-\overrightarrow{FE}.\overrightarrow{FH}+\overrightarrow{EF}.\overrightarrow{EA}+\overrightarrow{FG}.\overrightarrow{FH}+\overrightarrow{FG}.\overrightarrow{GC}$
    $E$ est le projeté orthogonal de $H$ sur $(FE)$ donc $\overrightarrow{FE}.\overrightarrow{FH}=FE^2=a^2$
    $(FE)$ et $(EA)$ sont perpendiculaires donc $\overrightarrow{EF}.\overrightarrow{EA}=0$
    $G$ est le projeté orthogonal de $H$ sur $(FG)$ donc $\overrightarrow{FG}.\overrightarrow{FH}=FG^2=a^2$
    $(FG)$ et $(GC)$ sont perpendiculaires donc $\overrightarrow{FG}.\overrightarrow{GC}=0$
    donc $\overrightarrow{EG}.\overrightarrow{FD}=-a^2+0+a^2+0=0$
  2. Calculer $\overrightarrow{EB}.\overrightarrow{FD}$.

    Aide

    $\overrightarrow{EB}=\overrightarrow{EF}+\overrightarrow{FD}$

    Solution

    $\overrightarrow{EB}.\overrightarrow{FD}$
    $=(\overrightarrow{EF}+\overrightarrow{FB}).(\overrightarrow{FH}+\overrightarrow{HD})$
    $=\overrightarrow{EF}.\overrightarrow{FH}+\overrightarrow{EF}.\overrightarrow{HD}+\overrightarrow{FB}.\overrightarrow{FH} +\overrightarrow{FB}.\overrightarrow{HD}$
    $=-\overrightarrow{FE}.\overrightarrow{FH}+\overrightarrow{EF}.\overrightarrow{EA}+\overrightarrow{FB}.\overrightarrow{FH} +\overrightarrow{FB}.\overrightarrow{FB}$
    $\overrightarrow{FE}.\overrightarrow{FH}=a^2$ (voir question 1)
    $(EF)$ et $EA)$ sont perpendiculaires donc $\overrightarrow{EF}.\overrightarrow{EA}=0$
    $(FB)$ et $(FH)$ sont perpendiculaires donc $\overrightarrow{FB}.\overrightarrow{FH}=0$
    $\overrightarrow{EB}.\overrightarrow{FD}=-a^2+0+0+a^2=0$
  3. En déduire que le plan $(EBG)$ est perpendiculaire à la droite $(FD)$.

    Rappel de cours

    droite et plan orthogonaux

    Une droite $(d)$ est orthogonale à un plan si et seulement si un vecteur directeur de $(d)$ est orthogonal à deux vecteurs directeurs de du plan.

    Aide

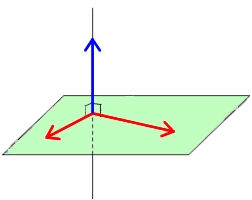    Il faut justifier que $(FD)$ est orthogonale à deux droites sécantes du plan $(EBG)$

    Solution

    $\overrightarrow{FD}.\overrightarrow{EG}=0$ donc $(FD)$ et $(EG)$ sont orthogonales
    $\overrightarrow{EB}.\overrightarrow{FD}=0$ donc $(EB)$ et $(FD)$ sont orthogonales
    donc $(FD)$ est orthogonale à deux droites sécantes du plan $(EBG)$

Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)

exercices semblables


Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
nº1342 Produit scalaire dans un cube
| 8-12mn |
nº1344 Droite et plan orthogonaux
| 8-10mn |
nº1348 Produit scalaire et orthogonalité
| 15-20mn |