Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
Dans chaque cas, déterminer la limite en $+\infty$ et $-\infty$.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
- $f(x)=\dfrac{x^2-2}{x-2}$ définie sur $\mathbb{R}\setminus\lbrace 2 \rbrace$.
Cas d'indétermination
$+\infty-\infty$
$0\times \pm \infty$
$\dfrac{\pm \infty}{\pm \infty}$
$\dfrac{0}{0}$
Attention, les écritures ci-dessus remplacent les limites mais sont incorrectes...En $-\infty$ et $+\infty$, il y a un cas d'indétermination donc il faut factoriser par le terme de plus haut degré au numérateur et au dénominateur soit $x^2$ au numérateur et $x$ au dénominateur.$f(x)=\dfrac{x^2\left(1-\dfrac{2}{x^2}\right)}{x\left(1-\dfrac{2}{x}\right)}$ (termes de plus haut degré en facteur)
$\phantom{f(x)}=\dfrac{x \left(1-\dfrac{2}{x^2}\right)}{1-\dfrac{2}{x}}$
Limite en $-\infty$
Par somme, $\displaystyle \lim_{x \rightarrow -\infty}1-\dfrac{2}{x^2}=1$ et $\displaystyle \lim_{x \rightarrow -\infty}x=-\infty$
donc par produit $\displaystyle \lim_{x \rightarrow -\infty}x\left(1-\dfrac{2}{x^2}\right)=-\infty$
et $\displaystyle \lim_{x \rightarrow -\infty}1-\dfrac{2}{x}=1$
Limite en $+\infty$
Par somme, $\displaystyle \lim_{x \rightarrow +\infty}1-\dfrac{2}{x^2}=1$ et $\displaystyle \lim_{x \rightarrow +\infty}x=+\infty$
donc par produit $\displaystyle \lim_{x \rightarrow +\infty}x\left(1-\dfrac{2}{x^2}\right)=+\infty$
et $\displaystyle \lim_{x \rightarrow +\infty}1-\dfrac{2}{x}=1$
- $f(x)=\dfrac{x^2-2}{x^3+3x+6}$ définie sur $\mathbb{R}$ et interpréter graphiquement le résultat obtenu (asymptote).
limite $l$ en $+\infty$ et interprétation graphique
La fonction $f$ est définie sur un intervalle $[a;+\infty[$ et $\ell \in \mathbb{R}$.
$\displaystyle \lim_{x \rightarrow +\infty}f(x)=\ell$ si pour tout intervalle ouvert I contenant $\ell$, il existe $x_0$ tel que pour tout $x>x_0$ on a $f(x)\in $ I
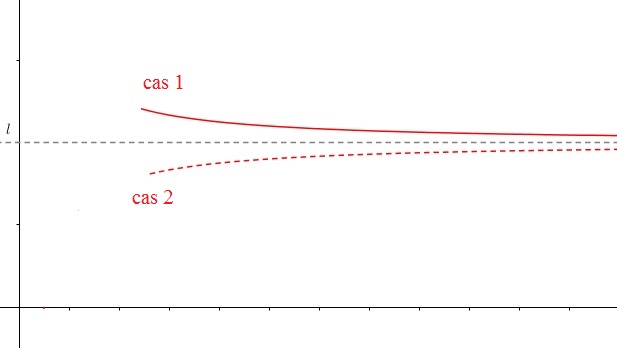
La droite d'équation $y=\ell$ est asymptote à la courbe en $+\infty$En $-\infty$ et $+\infty$, il y a un cas d'indétermination (quotient de deux limites infinies) donc il faut factoriser par le terme de plus haut degré au numérateur et au dénominateur soit $x^2$ au numérateur et $x$ au dénominateur.$f(x)=\dfrac{x^2\left(1-\dfrac{2}{x^2}\right)}{x^3\left(1+\dfrac{3}{x^2}+\dfrac{6}{x^3}\right)}$ (termes de plus haut degré en facteur)
$\phantom{f(x)}=\dfrac{1-\dfrac{2}{x^2}}{x\left(1+\dfrac{3}{x^2}+\dfrac{6}{x^3}\right)}$
Limite en $-\infty$
Par somme $\displaystyle \lim_{x \rightarrow -\infty}1-\dfrac{2}{x^2}=1$
Par somme $\displaystyle \lim_{x \rightarrow -\infty}1+\dfrac{3}{x^2}+\dfrac{6}{x^3}=1$ et $\displaystyle \lim_{x \rightarrow -\infty}x=-\infty$
donc par produit $\displaystyle \lim_{x \rightarrow -\infty}x\left(1+\dfrac{3}{x^2}+\dfrac{6}{x^3}\right)=-\infty$
Limite en $+\infty$
Par somme $\displaystyle \lim_{x \rightarrow +\infty}1-\dfrac{2}{x^2}=1$
Par somme $\displaystyle \lim_{x \rightarrow +\infty}1+\dfrac{3}{x^2}+\dfrac{6}{x^3}=1$ et $\displaystyle \lim_{x \rightarrow +\infty}x=+\infty$
donc par produit $\displaystyle \lim_{x \rightarrow +\infty}x\left(1+\dfrac{3}{x^2}+\dfrac{6}{x^3}\right)=+\infty$
L'axe des abscisses est donc une asymptote à la courbe en $+\infty$.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
