Une usine de composants électriques dispose de deux unités de production, A et B.
La production journalière de l'usine A est de $600$ pièces, celle de l'unité B est de $900$ pièces.
On prélève au hasard un composant de la production d'une journée.
La probabilité qu'un composant présente un défaut de soudure sachant qu'il est produit par l'unité A est égale à $0,014$.
La probabilité qu'un composant présente un défaut de soudure sachant qu'il est produit par l'unité B est égale à $0,024$.
On note :
- $D$ l'évènement : "le composant présente un défaut de soudure"
- $A$ l'évènement : "le composant est produit par l'unité A"
- $B$ l'évènement : "le composant est produit par l'unité B"
On note $p(D)$ la probabilité de l'évènement $D$ et $p_{A}(D)$ la probabilité de l'évènement $D$ sachant que l'évènement $A$ est réalisé.

Partie A : généralités

1. 1. D'après les données de l'énoncé, préciser $p_{A}(D)$ et $p_{B}(D)$.

      Rappel de cours

      Probabilité conditionnelle

      ---

      Soient $A$ et $B$ deux événements avec $p(A)\neq 0$.
      La probabilité que l'événement $B$ soit réalisé sachant que l'événement $B$ est réalisé se note $p_A(B)$
      et on a $p_A(B)=\dfrac{p(A\cap B)}{p(A)}$.

      Aide

      
      a notation $p_A(D)$ signifie que la pièce est produite dans l'usine dans l'usine A et on cherche la probabilité que cette pièce présente un défaut de soudure.

      Solution

      $p_A(D)$ est la probabilité qu'un composant présente un défaut de soudure (évènement $D$) sachant qu'il est produit dans l'usine A (évènement $A$), donc d'après l'énoncé avec $p_A(D)=0,014$.
      De même, $p_B(D)$ est la probabilité qu'un composant présente un défaut de soudure (évènement $D$) sachant qu'il est produit dans l'usine B (évènement $B$), avec $p_B(D)=0,024$.
      $p_A(D)=0,014$ et $p_B(D)=0,024$.
   2. Calculer $p(A)$ et $p(B)$.

      Aide

      Il faut déterminer le nombre de composaants fabriqués dans chaque usine par rapport au nombre total de composants produits.

      Solution

      Le nombre total de composants électriques fabriqués par les deux unités est $900 + 600 = 1500$ par jour.
      On en déduit donc que $p(A)=\dfrac{600}{1500}=0,4$
      et $p(B)=\dfrac{900}{1500}=1-0,4=0,6$
      $p(A)=0,4$ et $p(B)=0,6$.
   
   
2. Recopier et compléter l'arbre de probabilités ci-dessous :

   Rappel de cours

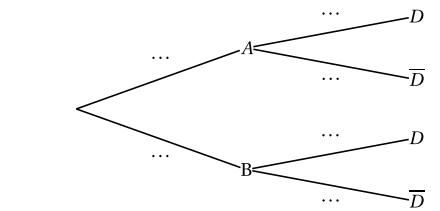
   Arbre pondéré

   ---

   Probabilités sur un arbre pondéré:
   

   Aide

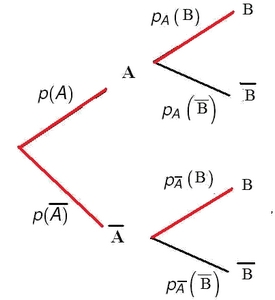   Sur le premier niveau de l'arbre, on a $p(A)$ et $P(B)$
   Sur le deuxième niveau de l'arbre, on a les probabilités conditionnelles $p_A(D)$, $p_A(\overline{D})$....

   Solution

   Arbre décrivant la situation:
   
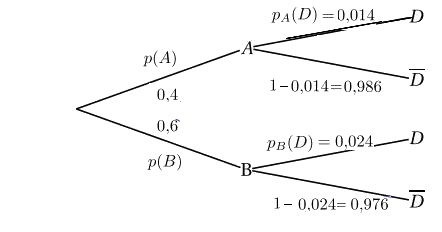
3. 1. Calculer $p(A \cap D)$ et $p(B \cap D)$.

      Rappel de cours

      Probabilité de l'événement $A\cap B$

      ---

      Soient $A$ et $B$ deux événements avec $p(A)\neq 0$, on a
      $p(A\cap B)=p(A)\times p_A(B)$

      Aide

      $p(A \cap D)$ est la probabilité d'avoir $A$ et $D$, c'est à dire que la pièce provienne de A et présente un défaut.

      Solution

      $p(A \cap D)=p(A)\times p_A(D)=0,4\times 0,014=0,0056$
      et $p(B\cap D)=p(B)\times p_B(D)=0,6\times 0,024=0,0144 $
      La probabilité que la pièce provienne de A et présente un défaut est $p(A \cap D)=0,0056$.
      La probabilité que la pièce provienne de B et présente un défaut est $p(B \cap D)=0,0144$.
   2. En déduire $p(D)$

      Rappel de cours

      Probabilités totales

      ---

      Soient $A_1$, $A_2$,...$A_n$ des événements de l'univers $\Omega$ tels que $p(A_1)\neq 0$, $p(A_2)\neq 0$...$p(A_n)\neq 0$ et $B$ un événements.
      Si $A_1$, $A_2$,...$A_n$ sont deux à deux disjoints et que leur réunion forme l'univers $\Omega$ alors $A_1$, $A_2$...$A_n$ forment une partition de $\Omega$
      et on a $p(B)=p(A_1\cap B)+p(A_2\cap B)+...+p(A_n\cap B)$}
      $A$ et $\overline{A}$ forment une partition de l'univers et on a $p(B)=p(A\cap B)+p(\overline{A}\cap B)$

      Aide

      Pour calculer $p(D)$, il faut utiliser sur l'arbre les parcours $A\capD$ et $B\cap D$

      Solution

      $A$ et $B=\overline{A}$ sont deux événements contraires
      donc $A\cap B=\oslash$ ($A$ et $B$ sont disjoints)
      $A\cup B=\Omega$
      donc $A$ et $B$ forment une partition de l'univers D'après la formule des probabilités totales, on a:
      $p(D) = p(A)\times p_A(D) + p(B)\times p_B(D)$
      $\phantom{p(D)}= p(A\cap D) + p(B\cap D) $
      $\phantom{p(D)}= 0,0056 + 0,0144$
      $\phantom{p(D)}= 0,02 $
      La probabilité que le composant présente un défaut est $p(D)=0,02$.
4. On prélève dans la-production totale un composant présentant un défaut de soudure.
   Quelle est la probabilité qu'il provienne de l'unité A ?

   Rappel de cours

   Probabilité conditionnelle

   ---

   Soient $A$ et $B$ deux événements avec $p(A)\neq 0$.
   La probabilité que l'événement $B$ soit réalisé sachant que l'événement $B$ est réalisé se note $p_A(B)$
   et on a $p_A(B)=\dfrac{p(A\cap B)}{p(A)}$.

   Aide

   On prélève dans la-production totale un composant présentant un défaut de soudure donc on sait que la pièce a un défaut.
   On peut utiliser $p(D)$ et $p_A(D)$ avec la formule des probabilités conditionnelles.

   Solution

   On prélève dans la-production totale un composant présentant un défaut de soudure donc on sait que la pièce a un défaut
   donc on veut calculer la probabilité que la pièce provienne de A sachant qu'elle a un défaut notée $p_D(A)$
   
   $p(A\cap D)=p(A)\times p_A(D)=p(D)p_D(A)$
   on a donc $p_D(A)=\dfrac{p(A\cap D)}{p(D)}=\dfrac{0,0056}{0,02}=0,28$
   La probabilité que la pièce provienne de A sachant qu'elle a un défaut est 0,28.