Publications MATHS-LYCEE.FR
Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
Lors de l'année de terminale ES, les trois quarts des élèves travaillent sérieusement tout au long de l'année scolaire.
Un candidat au baccalauréat ES a une probabilité de $0,9$ d'obtenir son bac s'il a travaillé sérieusement et une probabilité de $0,2$ s'il n'a pas travaillé sérieusement pendant l'année scolaire.
On note :
- T l'évènement "le candidat a travaillé sérieusement"
- A l'évènement " le candidat est admis au baccalauréat ES"
On interroge au hasard un candidat au baccalauréat ES.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Un candidat au baccalauréat ES a une probabilité de $0,9$ d'obtenir son bac s'il a travaillé sérieusement et une probabilité de $0,2$ s'il n'a pas travaillé sérieusement pendant l'année scolaire.
On note :
- T l'évènement "le candidat a travaillé sérieusement"
- A l'évènement " le candidat est admis au baccalauréat ES"
On interroge au hasard un candidat au baccalauréat ES.
- Construire un arbre pondéré traduisant les données de l'énoncé.
Probabilité conditionnelle
Soient $A$ et $B$ deux événements avec $p(A)\neq 0$.
La probabilité que l'événement $B$ soit réalisé sachant que l'événement $B$ est réalisé se note $p_A(B)$
et on a $p_A(B)=\dfrac{p(A\cap B)}{p(A)}$.Arbre pondéré
Probabilités sur un arbre pondéré:
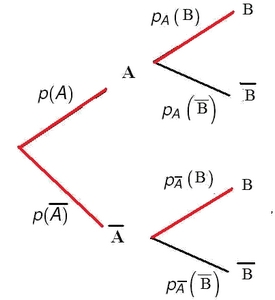Traduire les données de l'énoncé avec les notations des événements et des probabilités
Placer au premier niveau de l'arbre l'événement dont la probabilité donnée dans l'énoncé n'est pas une probabilité conditionnelleLes trois quarts des élèves travaillent sérieusement tout au long de l'année scolaire
donc $p(T)=\dfrac{3}{4}=0,75$.
Un candidat au baccalauréat ES a une probabilité de $0,9$ d'obtenir son bac s'il a travaillé sérieusement se traduit par le candidat a la probabilité 0,9 d'obtenir le BAC sachant qu'il a travaillé sérieusement
donc $p_T(A)=0,9$.
Un candidat au baccalauréat ES a une probabilité de $0,2$ d'obtenir son bac s'il n'a pas travaillé sérieusement se traduit par le candidat a la probabilité 0,2 d'obtenir le BAC sachant qu'il n'a pas travaillé sérieusement
donc $p_{\overline{T}}(A)=0,2$.
On a donc:
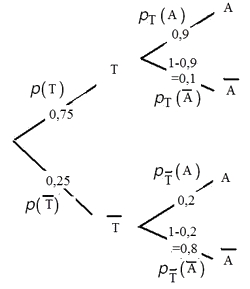
On place au premier niveau de l'arbre l'événement dont la probabilité n'est pas une probabilité conditionnelle (voir rappel cours). - Donner la signification et déterminer la probabilité de l'événement $T\cap A $
Probabilité de l'événement $A\cap B$
Soient $A$ et $B$ deux événements avec $p(A)\neq 0$, on a
$p(A\cap B)=p(A)\times p_A(B)$Identifier le parcours sur l'arbre correspondant à $T\cap A $ et effectuer le produit des coefficients.$T\cap A $ se lit $A$ et $T$ et est l'événement "le candidat a travaillé sérieusement et a obtenu le BAC".
$p(T\cap A)=p(T)\times p_T(A)=0,75\times 0,9=0,675$
- Donner la signification et déterminer la probabilité de l'événement $T \cap \overline{A}$
Identifier le parcours sur l'arbre correspondant à $T \cap \overline{A}$ et effectuer le produit des coefficients.$T \cap \overline{A}$ se lit $\overline{A}$ et $T$ et est l'événement "le candidat a travaillé sérieusement et n'a pas obtenu le BAC".
$p(T \cap \overline{A})=p(T)\times p_T( \overline{A})=0,75\times 0,1=0,075$
- Donner la signification et déterminer la probabilité de l'événement $\overline{T}\cap A$.
$\overline{T}\cap A$ se lit $\overline{T}$ et $A$ et est l'événement "le candidat n'a pas travaillé sérieusement et a obtenu le BAC".
$p(\overline{T}\cap A)=p(\overline{T})\times p_{\overline{T}}( A)=0,25\times 0,2=0,05$
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.