Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
Un site d'annonces sur internet a fait une étude sur la longueur des messages dans les annonces. Les résultats sont donnés dans les deux tableaux ci-dessous.
Le premier tableau donne le nombre de lignes dans la rubrique "ventes immobilières" et le second dans la rubrique "locations saisonnières".
Ventes immobilières

Locations saisonnières

Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Le premier tableau donne le nombre de lignes dans la rubrique "ventes immobilières" et le second dans la rubrique "locations saisonnières".
Ventes immobilières

Locations saisonnières

- Pour les ventes immobilières, quel est le pourcentage de variation du nombre d'annonces quand on passe de 6 à 10 lignes?
Taux d'évolution
Le taux d'évolution d'une valeur initiale $V_i$ à une valeur finale $V_f$ est la variation relative de l'évolution par rapport à la valeur initiale soit: $t=\dfrac{V_f-V_i}{V_i}$. En calculant $t\times 100$ on obtient le pourcentage d'évolution.On passe de 25 à 22 annoncesPour 6 lignes on a 25 annonces et pour 10 lignes on a 22 annonces.
Le taux de variation est donc $t=\dfrac{22-25}{25}=-0,12$
soit $-12$%
- Pour chaque série de données, calculer la moyenne arrondie aux dixièmes.
Donner la signification de la moyenne dans chacun des deux cas.Moyenne
On considère la série de $N$ données $x_i$ ($i$ entier naturel compris entre $1$ et $N$) les valeurs du caractère et $n_i$ les effectifs correspondants.
$N=n_1+n_2+$.... est l'effectif total.
La moyenne de la série statistique est $\overline{x}=\dfrac{n_1x_1+n_2x_2+\text{.....}+n_px_p}{N}$.} Dans le cas d'une série regroupée en classe, on utilise le centre des classes pour faire le calcul de la moyenne.On utilise le MENU STAT de la calculatrice.
et les listesAvec CASIO et le menu STAT de la calculatrice (voir cours calculatrices pour les autres modèles), on entre les listes correspondant au nombre de lignes LISTE1 puis au nombre d'annonces (effectif) en 2008 dans la LISTE2.
Paramétrer dans SET les données utilisées.
Pour faire les calculs pour l'année 2008, paramétrer 1VAR X: LIST1 et 1VAR Freq:LIST2
Pour les ventes immobilières, on obtient $\overline{x}\approx 8,1$.
Pour les locations saisonnières, on obtient $\overline{x'}\approx 5$ .
- Déterminer la médiane puis le premier et troisième quartile pour chaque série de données en justifiant les résultats donnés pour au moins l'une des deux séries.
Médiane
La médiane $M$ est la valeur du caractère telle que a 50% (la moitié) des valeurs soient inférieures ou égales à $M$ et l'autre moitié supérieures ou égale à $M$.
Exemple 1: Si l'effectif total est pair (par exemple 14 valeurs) alors la médiane est entre la 7ième et la 8ième valeur(valeurs classées dans l'ordre croissant)
Exemple 2: Si l'effectif total est impair (par exemple 15 valeurs) alors la médiane correspond à la 8ième valeur(valeurs classées dans l'ordre croissant)Quartiles
Le premier quartile $Q_1$ est la plus petite valeur du caractère telle que au moins 25% (un quart) des valeurs soient inférieures ou égales à $Q_1$.
Le troisième quartile $Q_3$ est la plus petite valeur du caractère telle que au moins 75% (trois quarts) des valeurs soient inférieures ou égales à $Q_3$.
L'intervalle $[Q_1;Q_3]$ est l'intervalle interquartile et $Q_3-Q_1$ est l'écart interquartile.On peut calculer et tiliser les effectifs cumulés croissants.En complétant les tableaux avec les effectifs cumulés croissants, on a:
Ventes immobilières

L'effectif total est pair et $\dfrac{170}{2}=85$ donc la médiane est comprise entre la 85ième valeur et la 86ième valeur
La 85ième valeur est 8 et la 86ième également (colonne en rouge dans le tableau) donc la médiane est 8
cela signifie que la moitié des annonces ont 8 lignes ou moins et l'autre moitié 8 lignes ou plus.
Le quart de l'effectif total est $\dfrac{170}{4}=42,5$ donc le premier quartile $Q_1$ correspond à la 43ième valeur soit $Q_1=7$ (colonne en bleu dans le tableau).
Trois quarts de l'effectif total est égal à $\dfrac{3\times 170}{4}=127,5$ donc le troisième quartile $Q_3$ correspond à la 128ième valeur soit $Q_3=9$ (colonne en vert dans le tableau).
Locations saisonnières

$\dfrac{149}{2}=74,5$ donc la médiane est la 75ième valeur soit $ med'=5$.
De même que pour le premier tableau, $\dfrac{149}{4}=37,25$ donc $Q'_1=4$
et $\dfrac{3\times 149}{4}=117,5$ donc $Q'_3=6$
- Construire les deux diagrammes en boîte puis commenter ces résultats.
Diagramme en boîte
Sur un axe gradué, on doit placer le minimum, $Q_1$, médiane, $Q_3$ et la valeur maximale.
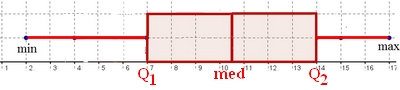 Comparer les moyennes puis les médianes et l'écart interquartile ("taille" de la boîte)Il faut utiliser un axe gradué de 3 à 12 (nombre de lignes).
Comparer les moyennes puis les médianes et l'écart interquartile ("taille" de la boîte)Il faut utiliser un axe gradué de 3 à 12 (nombre de lignes).
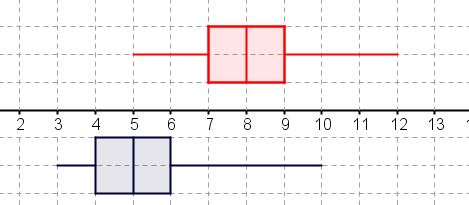
Il en est de même pour l'écart entre le premier et troisième quartiles donc on peut en conclure que la répartition des données est sensiblement la même pour les deux s d'annonces mais que le nombre de lignes est nettement inférieur pour les locations saisonnières.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Fiche méthode
Si cet exercice vous pose problème, nous vous conseillons de consulter la fiche méthhode.
Médianes et quartiles avec une série discrète
- définitions
- méthode
- exemple
infos: | 10mn |
vidéos semblables
Pour compléter cet exercice, nous vous conseillons les vidéos suivantes semblables à l'exercice affiché.
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
