Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
- Calculer $AB$ et $AJ$
Théorème de Thalès
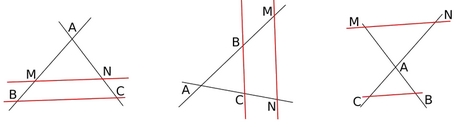
Soit un triangle $ABC$ et deux points $M$ et $N$ des droites $(AB)$ et $(AC)$ de sorte que la droite $(BC)$ soit parallèle à la droite $(MN)$ (voir figures)
alors $\dfrac{AB}{AM}=\dfrac{AN}{AC}=\dfrac{MN}{BC}$
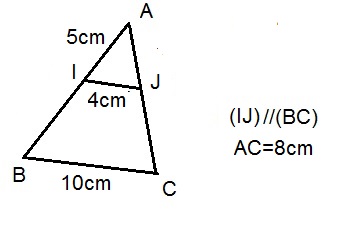
 On peut utiliser les parallèles $(IJ)//(BC)$ pour appliquer le théorème de ThalèsDans le triangle $ABC$ on a $I\in [AB]$ et $J\in [AC]$ et $(IJ)//(BC)$.
On peut utiliser les parallèles $(IJ)//(BC)$ pour appliquer le théorème de ThalèsDans le triangle $ABC$ on a $I\in [AB]$ et $J\in [AC]$ et $(IJ)//(BC)$.
Avec le théorème de Thalès, on peut écrire:
$\dfrac{AI}{AB}=\dfrac{AJ}{AC}=\dfrac{IJ}{BC}$
donc en remplaçant par les longueurs données, on a: $\dfrac{5}{AB}=\dfrac{AJ}{8}=\dfrac{4}{10}$
- Calcul de $AB$
$\dfrac{5}{AB}=\dfrac{2}{5}$ (on peut simplifier la fraction $\dfrac{4}{10}$)
donc $2AB=25$ (produits en croix égaux)
- calcul de $AJ$
$\dfrac{AJ}{8}=\dfrac{2}{5}$
donc $AJ=\dfrac{2}{5}\times 8=\dfrac{16}{5}$
- Calculer $AC$ puis $AD$.
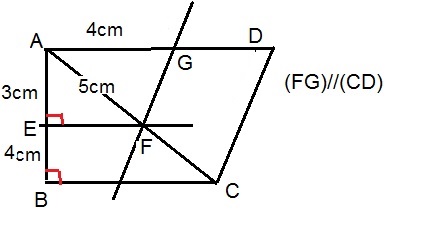 On peut utiliser les parallèles $(EF)//(BC)$ pour appliquer le théorème de Thalès- Calcul de $AC$
On peut utiliser les parallèles $(EF)//(BC)$ pour appliquer le théorème de Thalès- Calcul de $AC$
Données: $(BC)\perp (AB)$ et $(EF)\perp (AB)$
propriétés: Si deux droites sont perpendiculaires à une même troisième alors elles sont perpendiculaires entre-elles.
Conclusion:
Dans le triangle $ABC$ on a $E\in [AB]$ et $F\in [AC]$ et $(EF)//(BC)$.
Avec le théorème de Thalès, on peut écrire:
$\dfrac{AE}{AB}=\dfrac{AF}{AC}=\dfrac{EF}{BC}$
donc en remplaçant par les longueurs données, on a: $\dfrac{3}{7}=\dfrac{5}{AC}=\dfrac{EF}{BC}$
( $AB=AE+EB=3+4=7$cm)
donc $3AC=7\times 5$ (produits en croix égaux)
- Calcul de $AD$
Dans le triangle $ACD$ on a $F\in [AC]$ et $G\in [AD]$ et $(FG)//(CD)$.
Avec le théorème de Thalès, on peut écrire (rappel, dans le premier calcul on a $\dfrac{AF}{AC}=\dfrac{3}{5}$):
$\dfrac{AF}{AC}=\dfrac{AG}{AD}=\dfrac{FG}{CD}$
donc en remplaçant par les longueurs données, on a: $\dfrac{3}{5}=\dfrac{4}{AD}=\dfrac{FG}{CD}$
donc $3AD=4\times 5$ (produits en croix égaux)
Pour le second calcul, on a juste besoin du rapport $\dfrac{AF}{AD}=\dfrac{3}{5}$ donc on peut finalement éviter le calcul de $AC$
La fraction $\dfrac{20}{3}$ ne peut s'écrire sous forme d'un nombre décimal donc on doit laisser cette longueur écrite sous forme fractionnaire.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Fiche méthode
Si cet exercice vous pose problème, nous vous conseillons de consulter la fiche méthhode.
Rappels de collège
- théorème de Thalès
- théorème de Pythagore
- trigonométrie dans le triangle rectangle
- droites du triangle (hauteurs, médiatrices et médianes)
infos: | 10-15mn |
