Une entreprise fabrique des appareils électroniques de haute technologie.
Le coût total de fabrication de $q$ appareils est $C(q)=q^2+40q+125$.
Le coût est exprimé en centaines d'euros avec $q\in[0;40]$.
On admet que chaque appareil fabriqué est vendu au prix unitaire de 7000 euros et que toute la production est vendue.
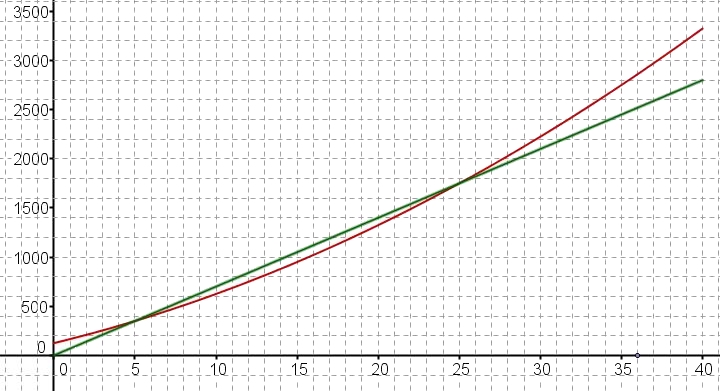
La figure ci-dessous, donne la courbe représentative de la fonction coût total dans un repère orthogonal.

1. Exprimer la recette $R(q)$, en centaines d'euros en fonction de $q$.

   Aide

   chercher le prix de vente, en centaines d'euros, d'un appareil puis celui de $q$ appareils.

   Solution

   Chaque appareil est vendu 7000 euros soit 70 centaines d'euros.
   donc pour $q$ appareils, cela donne une recette de $70q$ centaines d'euros.
   
   $R(q)=70q$
2. Tracer la représentation graphique de la fonction $R$ dans le repère ci-dessous.

   Aide

   $R$ est une fonction linéaire donc la représentation graphique de $R$ est un segment ($x\in [0;40]$).

   Solution

   $R$ est une fonction linéaire et la représentation graphique de $R$ passe donc par l'origine du repère et par le point de coordonnées $(20;1400)$ par exemple.
   
3. Exprimer le bénéfice $B(q)$, en centaines d'euros, en fonction de $q$.

   Aide

   Le bénéfice est égal à la recette diminuée des coûts de fabrication.

   Solution

   $B(q)=R(q)-C(q)$
   $\phantom{B(q)}=70q-(q^2+40q+125)$ (attention à mettre $C(q)$ entre parenthèses)
   $\phantom{B(q)}=70q-q^2-40q-125$
   $\phantom{B(q)}=-q^2+30q-125$
   
   $B(q)=-q^2+30q-125$ centaines d'euros.
4. Résoudre graphiquement l'équation $B(q)=0$ et vérifier ensuite par le calcul que les solutions obtenues sont correctes.

   Aide

   On veut déterminer les abscisses des points pour lesquelles la recette est égale au coût de fabrication.

   Solution

   Le bénéfice est nul lorsque $R(q)=C(q)$ donc les solutions de l'équation $B(q)=0$ sont les abscisses des points d'intersection de la courbe représentant la fonction $C$ et du segment représentant la fonction $R$.
   
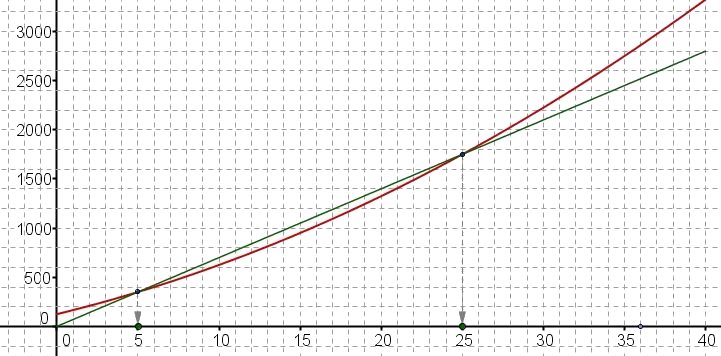
   donc $B(q)=0$ pour $q=5$ ou $q=25$
   
   $B(q)=0$ pour $q=5$ ou $q=25$.
   On peut contrôler l'exactitude des lectures graphiques en calculant l'image par $B$ de 5 puis de 25.
   $B(5)=-5^2+30\times 5-125=-25+150-125=0$ et $B(25)=-25^2+30\times 25-125=-625+750-125=0$
5. En utilisant la question précédente et le graphique, déterminer la quantité d'appareils à produire pour que l'entreprise ne soit pas en déficit.

   Aide

   Il faut déterminer les valeurs de $q$ pour lesquelles on a un bénéfice positif soit $B(q)>0$ donc pour lesquelles $R(q)$ est supérieur ou égal à $C(q)$

   Solution

   Graphiquement, les solutions de l'inéquation $B(q)\geq 0$, c'est à dire de $R(q)\geq C(q)$ sont les abscisses des points de la courbe représentant $R$ situés au-dessus de la courbe représentant $B$ (zone en pointillés bleus sur le graphique)
   
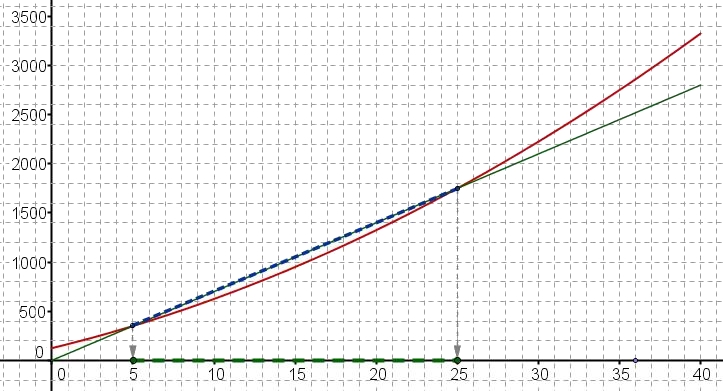
   On a donc $R(q)\geq C(q)$ pour $q\in [5;25]$ (zone en pointillés verts sur le graphique)
   
   L'entreprise n'est pas en déficit si elle produit entre 5 et 25 appareils.