Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
$ABCD$ est un parallélogramme et les points E et F sont définies par les relations
$\overrightarrow{AE}=3\overrightarrow{AB}$ et $\overrightarrow{DF}=\dfrac{1}{2}\overrightarrow{BC}$
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
$\overrightarrow{AE}=3\overrightarrow{AB}$ et $\overrightarrow{DF}=\dfrac{1}{2}\overrightarrow{BC}$
- Construire la figure en plaçant tous les points de l'énoncé
Pour construire le point $E$, il faut effectuer la translation de vecteur $3\overrightarrow{AB}$ en partant du point $A$
Pour construire le point $F$, il faut effectuer la translation de vecteur $\dfrac{1}{2}\overrightarrow{BC}$ en partant du point $D$Le point $E$ est l'image du point $A$ par la translation $3\overrightarrow{AB}$
Le point $F$ est l'image du point $D$ par la translation $\dfrac{1}{2}\overrightarrow{BC}=\dfrac{1}{2}\overrightarrow{AD}$
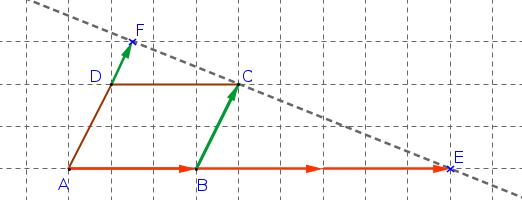
- Montrer que les points $C$, $E$ et $F$ sont alignés.
On pourra décomposer les vecteurs $\overrightarrow{CE}$ et $\overrightarrow{CF}$ en fonction de vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AD}$ par exemple ou bien utiliser une méthode analytique en choisissant un repère formé avec les côtés du parallélogramme.Il faut montrer que les vecteurs $\overrightarrow{CE}$ et $\overrightarrow{CF}$ par exemple sont colinéaires
En utilisant les vecteurs, on peut exprimer les vecteurs $\overrightarrow{CE}$ et $\overrightarrow{CF}$ en fonction de $\overrightarrow{AB}$ et $\overrightarrow{AD}$Première méthode: méthode vectorielle
ABCD est un parallélogramme donc $\overrightarrow{AB}=\overrightarrow{DC}$ et $\overrightarrow{BC}=\overrightarrow{AD}$
$\overrightarrow{CE}=\overrightarrow{CB}+\overrightarrow{BE}$
$\phantom{\overrightarrow{CE}}=-\overrightarrow{AD}+\overrightarrow{BA}+\overrightarrow{AE}$
$\phantom{\overrightarrow{CE}}=-\overrightarrow{AD}+\overrightarrow{BA}+3\overrightarrow{AB}$
$\phantom{\overrightarrow{CE}}=-\overrightarrow{AD}-\overrightarrow{AB}+3\overrightarrow{AB}$
$\phantom{\overrightarrow{CE}}=2\overrightarrow{AB}-\overrightarrow{AD}$
$\overrightarrow{CF}=\overrightarrow{CD}+\overrightarrow{DF}$
$\phantom{\overrightarrow{CF}}=-\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{BC}$
$\phantom{\overrightarrow{CF}}=-\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}$
$-2\overrightarrow{CF}=-2(-\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD})=2\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{CE}$
donc les vecteurs $\overrightarrow{CF}$ et $\overrightarrow{CE}$ sont colinéaires
Seconde méthode: méthode analytique
En utilisant le repère $(A;\overrightarrow{AB};\overrightarrow{AD})$, on a $A(0;0)$, $B(1;0)$, $C(1;1)$ et $D(0;1)$
$\overrightarrow{AE}=3\overrightarrow{AB}$ donc:
$\begin{cases} x_E-x_A=\dfrac{1}{3}(x_B-x_A)\\ y_E-y_A=\dfrac{1}{3}(y_B-y_A) \end{cases}\Longleftrightarrow \begin{cases} x_E=3\\ y_E=0 \end{cases}$ donc $E(3;0)$
$\overrightarrow{DF}=\dfrac{1}{2}\overrightarrow{BC}$ donc:
$\begin{cases} x_F-x_D=\dfrac{1}{2}(x_C-x_B)\\ y_F-y_D=\dfrac{1}{2}(y_C-y_B) \end{cases}\Longleftrightarrow \begin{cases} x_F-0=\dfrac{1}{2}\times 0\\ y_F-1=\dfrac{1}{2}\times 1 \end{cases}$
$\phantom{\begin{cases} x_F-x_D=\dfrac{1}{2}(x_C-x_B) \\ y_F-y_D=\dfrac{1}{2}(y_C-y_B) \end{cases}}\Longleftrightarrow \begin{cases} x_F=0 \\ y_F=\dfrac{3}{2} \end{cases}$
donc $F(0;\dfrac{3}{2})$
On peut aussi donner les coordonnées de $E$ directement avec la relation vectorielle:
$\overrightarrow{AE}=3\overrightarrow{AB}=3\overrightarrow{AB}+0\overrightarrow{AD}$ donc $E(3;0)$.
$\begin{cases} x_{\overrightarrow{CE}}=x_E-x_C=3-1=2 \\ y_{\overrightarrow{CE}}=y_E-y_C=0-1=-1 \end{cases}$ donc $\overrightarrow{CE}(2;-1)$
$\begin{cases} x_{\overrightarrow{CF}}=x_F-x_C=0-1=-1 \\ y_{\overrightarrow{CF}}=y_F-y_C=\dfrac{3}{2}-1=\dfrac{1}{2} \end{cases}$ donc $\overrightarrow{CF}(-1;\dfrac{1}{2})$
$x_{\overrightarrow{CE}}y_{\overrightarrow{CF}}- y_{\overrightarrow{CE}}x_{\overrightarrow{CF}}=2\times \dfrac{1}{2}-(-1)\times (-1)=1-1=0$
donc les vecteurs $\overrightarrow{CE}$ et $\overrightarrow{CF}$ sont colinéaires
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Fiche méthode
Si cet exercice vous pose problème, nous vous conseillons de consulter la fiche méthhode.
Vecteurs colinéaires et alignement
- montrer que trois points sont alignés dans un repère
- utiliser le critère de colinéarité
infos: | 10mn |
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.