Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
La fonction $f$ est définie sur $]0;+\infty[$ et pour tout réel $x> 1$ , on a $\dfrac{1}{x^2} < f(x) < \dfrac{1}{x}$
et que pour tout réel $x \in ]0;1[$, on a $\dfrac{1}{x} < f(x) < \dfrac{1}{x^2}$.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
et que pour tout réel $x \in ]0;1[$, on a $\dfrac{1}{x} < f(x) < \dfrac{1}{x^2}$.
- Déterminer $\displaystyle \lim_{x \rightarrow +\infty}f(x)$
Encadrement (théorème des "gendarmes")
$f$, $g$ et $h$ sont définies sur $I=]a;+\infty[$ telles que $f(x)\leq g(x)\leq h(x)$ sur $I$.
Si $\displaystyle \lim_{x \rightarrow +\infty}f(x)=\displaystyle \lim_{x \rightarrow +\infty}h(x)=l$ alors $\displaystyle \lim_{x \rightarrow +\infty}g(x)=l$On cherche d'abord $\displaystyle \lim_{x \rightarrow +\infty}\dfrac{1}{x}$ puis $\displaystyle \lim_{x \rightarrow +\infty}\dfrac{1}{x+1}$Pour tout réel $x > 0$, on pose $u(x)=\dfrac{1}{x^2}$ et $v(x)=\dfrac{1}{x}$
$\displaystyle \lim_{x \rightarrow +\infty}u(x)=\displaystyle \lim_{x \rightarrow +\infty}\dfrac{1}{x^2}=0$
et $\displaystyle \lim_{x \rightarrow +\infty}v(x)=\displaystyle \lim_{x \rightarrow +\infty}\dfrac{1}{x}=0$
et pour tout réel $x > 1$, on a $u(x) < f(x) < v(x)$
- Déterminer la limite de $f$ en 0.
Limite par comparaison
Soit $f$ et $g$ définie sur $I=]a;+\infty[$ telles que $f(x)\leq g(x)$ sur $I$.
Si $\displaystyle \lim_{x \rightarrow +\infty}f(x)=+\infty$ alors $\displaystyle \lim_{x \rightarrow +\infty}g(x)=+\infty$
Si $\displaystyle \lim_{x \rightarrow +\infty}g(x)=-\infty$ alors $\displaystyle \lim_{x \rightarrow +\infty}f(x)=-\infty$on peut chercher $\displaystyle \lim_{x \rightarrow 0^+} \dfrac{1}{x}$$\displaystyle \lim_{x \rightarrow 0^+} \dfrac{1}{x}=+\infty$
et pour tout réel $x\in ]0;1[$, on a $f(x) > u(x)$
Graphiquement, on a (courbe de $f$ en gris)
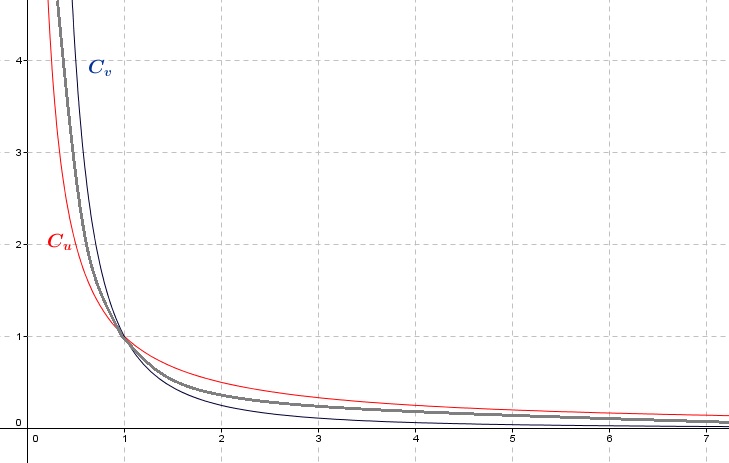
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
