1. Home
  2. chapitre 1 Second degré
  3. exercice corrigé nº632
PDF reservé aux abonnés
La fonction $f$ est définie sur $\mathbb{R}$ et est une fonction polynôme de second degré.
Dans chaque cas, déterminer l'expression de $f$, la représentation graphique $C_f$ de $f$ étant donnée.
  1. figure 1:

    Rappel de cours

    Forme factorisée

    - Si le polynôme du second degré $P(x)=ax^2+bx+c$ (avec $a\neq 0$) admet deux racines $x_1$ et $x_2$
    alors la forme factorisée de $P$ est $P(x)=a(x-x_1)(x-x_2)$

    - Si le polynôme du second degré $P(x)=ax^2+bx+c$ (avec $a\neq 0$) admet une racine $x_1$
    alors la forme factorisée de $P$ est $P(x)=a(x-x_1)^2$

    - Si le polynôme du second degré $P(x)=ax^2+bx+c$ (avec $a\neq 0$) n'admet aucune racine
    alors la forme factorisée de $P$ n'existe pas

    Aide

    On peut lire graphiquement les abscisses des points d'intersection de la courbe et de l'axe des abscisses
    donc on peut utiliser la forme factorisée de $f$
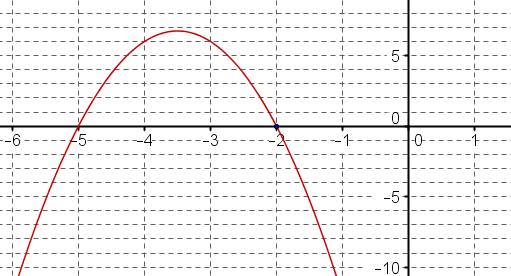
    $C_f$ passe par le point de coordonnées $(-3;6)$ donc $f(-3)=6$

    Solution

    La courbe coupe l'axe des abscisses en $x_1=-5$ et $x_2=-2$
    donc $x_1=-5$ et $x_2=-2$ sont les deux racines de $f$
    $f(x)=a(x-x_1)(x-x_2)=a(x+5)(x+2)$
    Le point de coordonnées $(-3;6)$ appartient à la courbe $C_f$
    donc $f(-3)=6$
    $f(-3)=6 \Longleftrightarrow a(-3+5)(-3+2)=6$
    $\phantom{f(-3)=6}\Longleftrightarrow -2a=6$
    $\phantom{f(-3)=6}\Longleftrightarrow a=-3$
  2. figure 2:

    Rappel de cours

    Forme canonique

    Toute fonction polynôme de degré 2 définie sur $\mathbb{R}$ par $P (x) = ax^2 + bx + c$ peut s'écrire sous la forme $P (x) = a(x -\alpha)^2 + \beta$ avec $\alpha=\dfrac{-b}{2a}$ et $\beta= P ( \alpha)$.
    Cette écriture de $P (x)$ est appelée forme canonique et $S(\alpha;\beta)$ est le sommet de la parabole représentant la fonction $P$

    Aide

    On peut lire graphiquement les coordonnées du sommet de la parabole
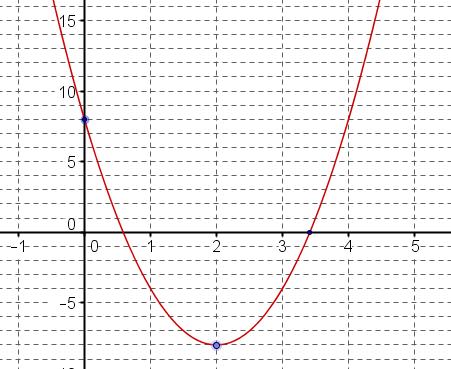
    Le point d'intersection de la parabole et de l'axe des ordonnées a pour coordonnées $(0;8)$.
    Il faut utiliser la forme canonique de $f$

    Solution

    Le sommet de la parabole $C_f$ a pour coordonnées $(2;-8)$
    La forme canonique de $f$ est $f(x)=a(x-\alpha)^2+\beta$ avec $\alpha=2$ et $\beta=-8$
    donc $f(x)=a(x-2)^2-8$
    Le point de coordonnées $(0;8)$ appartient à la courbe $C_f$
    donc $f(0)=8$
    $f(0)=8 \Longleftrightarrow a(0-2)^2-8=8$
    $\phantom{f(0)=-8}\Longleftrightarrow 4a-8=8$
    $\phantom{f(0)=-8}\Longleftrightarrow 4a=16$
    $\phantom{f(0)=-8}\Longleftrightarrow a=4$
  3. figure 3:

    Aide

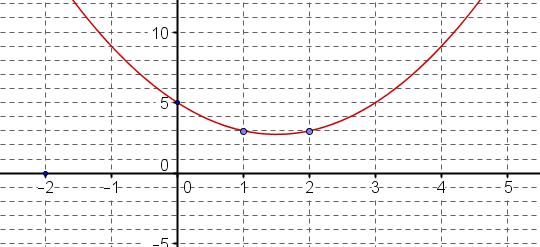    On peut lire graphiquement les coordonnées de trois points de la parabole
    Il faut utiliser la forme développée de $f$ et écrire un système d'équations avec les inconnues $a$, $b$ et $c$

    Solution

    La parabole $C_f$ passe par les points de coordonnées $(0;5)$, $(1;3)$ et $(2;3)$
    $f(x)=ax^2+bx+c$ et $f(0)=5$
    $f(0)=5 \Longleftrightarrow a\times 0^2+b\times 0+c=5 \Longleftrightarrow c=5$
    donc $f(x)=ax^2+bx+5$
    $f(1)=3 \Longleftrightarrow a\times 1^2+b\times 1+5=3$

    $\phantom{f(1)=3 } \Longleftrightarrow a+b=-2$

    $f(2)=3 \Longleftrightarrow a\times 2^2+b\times 2+5=3$

    $\phantom{f(2)=3 } \Longleftrightarrow 4a+2b=-2$ (on peut diviser les deux membres par 2)

    $\phantom{f(2)=3 } \Longleftrightarrow 2a+b=-1$
    Il faut donc résoudre le système d'équations:
    $\begin{cases} a+b=-2\\ 2a+b=-1 \end{cases}\Longleftrightarrow \begin{cases} b=-2-a\\ 2a-2-a=-1 \end{cases}$

    $\phantom{\begin{cases} a+b=-2\\ 2a+b=-1 \end{cases}} \Longleftrightarrow \begin{cases} b=-2-1\\ a=1 \end{cases}$

    $\phantom{\begin{cases} a+b=-2\\ 2a+b=-1 \end{cases}} \Longleftrightarrow \begin{cases} b=-3\\ a=1 \end{cases}$

devoir nº 662


Vous pouvez retourner sur le devoir après avoir vu cet exercice

Devoir complet fin de chapitre

- déterminer f à partir du graphique
- inéquations
- polynôme de degré 3
- recettes, coûts et bénéfices

infos cours

| 60mn

retour sur le devoir