1. Home
  2. chapitre 8 Équations de droites dans un repère
  3. exercice corrigé nº425
PDF reservé aux abonnés
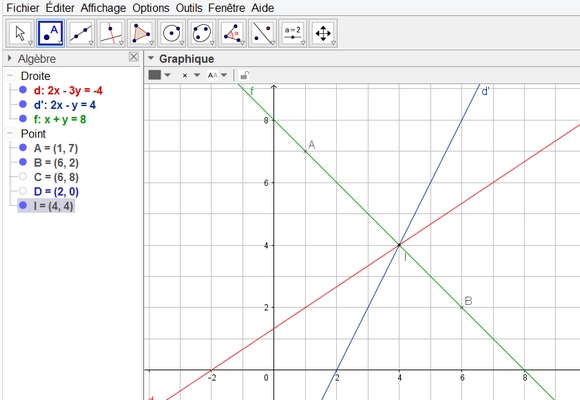
Dans un repère du plan, on donne la droite $(d)$ d'équation $2x-3y+4=0$, la droite $(d')$ d'équation $2x-y-4=0$ et les points $A(1;7)$ et $B(6;2)$.
  1. Déterminer une équation cartésienne de la droite $(AB)$.

    Rappel de cours

    Déterminer une équation cartésienne

    Déterminer une équation cartésienne de la droite $(AB)$ avec $A(x_A;y_A)$ et $B(x_B;y_B)$ donnés dans un repère.
    Méthode 1
    - calculer les coordonnée du vecteur $\overrightarrow{AB}$ vecteur directeur de $(AB)$
    - Si le point $M(x;y)$ appartient à $(AB)$, les vecteurs $\overrightarrow{AM}$ et $\overrightarrow{AB}$ sont colinéaires
    - $det(\overrightarrow{AM};\overrightarrow{AB})=0$

    Méthode 2
    - calculer les coordonnée du vecteur $\overrightarrow{AB}$ vecteur directeur de $(AB)$
    - Les coordonnées de $\overrightarrow{AB}(-b;a)$ donnent les coefficients $a$ et $b$ d'une équation cartésienne
    - $(AB)$: $ax+by+c=0$ et $A\in (AB)$ donc $ax_A+by_A+c=0$ (équation d'inconnue $c$)

    Solution

    $\begin{cases} x_B-x_A=6-1=5\\ y_B-y_A=2-7=-5\end{cases}$
    donc $\overrightarrow{AB}(5;-5)$ est un vecteur directeur de $(AB)$
    Méthode 1
    Soit $M(x;y)$ un point de $(AB)$, $\overrightarrow{AM}(x-1;y-7)$
    $\overrightarrow{AM}$ et $\overrightarrow{AB}$ sont colinéaires
    $\Longleftrightarrow det(\overrightarrow{AM};\overrightarrow{AB})=0$
    $\Longleftrightarrow \begin{bmatrix}x-1&5\\ y-7&-5\end{bmatrix}=0$
    $\Longleftrightarrow -5(x-1)-5(y-7)=0$
    $\Longleftrightarrow -5x-5y+40=0$
    $\Longleftrightarrow -x-y+8=0$ (en divisant tous les coefficients par $5$)

    Méthode 2
    $\overrightarrow{AB}(5;-5)$ est un vecteur directeur de $(AB)$ donc $a=-5$ et $b=-5$
    donc $(AB)$ admet une équation cartésienne de la forme $-5x-5y+c=0$
    $A\in (AB) \Longleftrightarrow -5\times 1-5\times 7+c=0 \Longleftrightarrow c=40$
  2. Justifier que les droites $(d)$ et $(d')$ ne sont pas parallèles puis calculer les coordonnées de $I$ point d'intersection de $(d)$ et $(d')$.

    Aide

    Il faut vérifier que les vecteurs directeurs ne sont pas colinéaires
    On peut résoudre le système d'équations par combinaisons ou par substitution en isolant $y$ dans la seconde équation

    Solution

    $\overrightarrow{u}(3;2)$ est un vecteur directeur de $(d)$
    $\overrightarrow{u'}(1;2)$ est un vecteur directeur de $(d')$
    $det(\overrightarrow{u};\overrightarrow{u'})=\left| \begin{array} {cc}3&2\\1&2\end{array}\right|=3\times 2-1\times 2=4\neq 0$
    donc $\overrightarrow{u}$ et $\overrightarrow{u'}$ ne sont pas colinéaires

    Il faut résoudre $\begin{cases} 2x-3y+4=0\\2x-y-4=0\end{cases}$
    $\phantom{\Longleftrightarrow} \begin{cases} 2x-3y+4=0\\2x-y-4=0\end{cases}$
    $\Longleftrightarrow \begin{cases} 2x-3y+4-(2x-y-4)=0~~~~~~~L_1-L_2\\2x-3y+4-3(2x-y-4)=0~~~~~L_1-3L_2\end{cases}$
    $\Longleftrightarrow \begin{cases} 2x-3y+4-2x+y+4=0\\2x-3y+4-6x+3y+12=0\end{cases}$
    $\Longleftrightarrow \begin{cases} -2y=-8\\-4x=-16\end{cases}$
    $\Longleftrightarrow \begin{cases} y=4\\x=4\end{cases}$

    Contrôle
    $2\times 4-3\times 4+4=8-12+4=0$
    $2\times 4-4-48-8=0$
  3. Montrer que les droites $(d)$, $(d')$ et $(AB)$ sont concourantes.

    Aide

    On peut vérifier que $I$ appartient aussi à $(AB)$

    Solution

    $-x-y+8=0$ est une équation cartésienne de $(AB)$
    $-x_I-y_I+8=-4-4+8=0$
    donc $I\in (AB)$

    Figure et tracés avec GEOGEBRA

devoir nº 435


Vous pouvez retourner sur le devoir après avoir vu cet exercice

Équations cartésiennes

- équation cartésienne d'une droite
- problème d'alignement en utilisant un repère
- équation avec un paramètre

infos cours

| 60mn

retour sur le devoir