En utilisant une intégration par parties, calculer les intégrales suivantes:
-
$I=\displaystyle \int_0^{2\pi} xsin(x) dx$
Primitives des fonctions usuelles
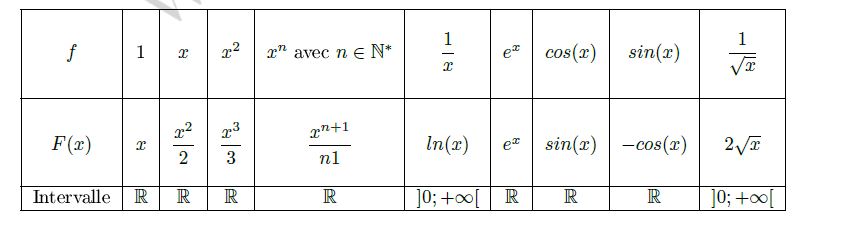
Intégration par parties
$u$ et $v$ sont deux fonctions dérivables sur $[1;b]$.
$\displaystyle \int_a^b u'v=[uv]_a^b-\int_a^b uv'$On pose $u'(x)=sin(x)$ et $v(x)=x$On pose $u'(x)=sin(x)$ et $v(x)=x$
On a alors $u(x)=-cos(x)$ et $v'(x)=1$
$I=\displaystyle \int_0^{2\pi} xsin(x) dx$
$=\displaystyle \int_0^{2\pi} u'(x)v(x) dx$
$=[u(x)v(x)]_0^{2\pi}-\displaystyle \int_0^{2\pi} u(x)v'(x)dx$
$=[-xcos(x)]_0^{2\pi}-\displaystyle \int_0^{2\pi} -cos(x)(x)dx$
$=-\pi cos(\pi)+0cos(0)-[-sin(x)]_0^{2\pi}$
$=1-(-sin(\pi)+sin(0))$
$=1$ (rappel $sin(0)=sin(\pi)=0$)
Penser à contrôler avec la calculatrice - $I=\displaystyle \int_0^{\dfrac{\pi}{2}}2xcos(x)dx$
On pose $u'(x)=cos(x)$ et $v(x)=2x$On pose $u'(x)=cos(x) $ et $v(x)=2x$
On a alors $u(x)=sin(x)$ et $v'(x)=2$
$I=\displaystyle \int_0^{\dfrac{\pi}{2}} 2xcos(x) dx$
$=\displaystyle \int_0^{\dfrac{\pi}{2}} u'(x)v(x) dx$
$=[u(x)v(x)]_0^{\dfrac{\pi}{2}}-\displaystyle \int_0^{\dfrac{\pi}{2}} u(x)v'(x)dx$
$=\left[2xsin(x)\right]_0^{\dfrac{\pi}{2}}-\displaystyle \int_0^{\dfrac{\pi}{2}} 2sin(x)dx$
$=2\times \dfrac{\pi}{2}sin\left(\dfrac{\pi}{2}\right)-2\times 0sin(0)-\left[-2cos(x)\right]_0^{\dfrac{\pi}{2}}$
$=\pi-\left(-2cos\left(\dfrac{\pi}{2}\right)+2cos(0)\right)$
$=\pi-2$
Penser à contrôler avec la calculatrice
devoir nº 1290
Vous pouvez retourner sur le devoir après avoir vu cet exercice
Calculs d'intégrales
- intégrales avec les fonctions usuelles
- intégration par parties
infos cours
| 30mn