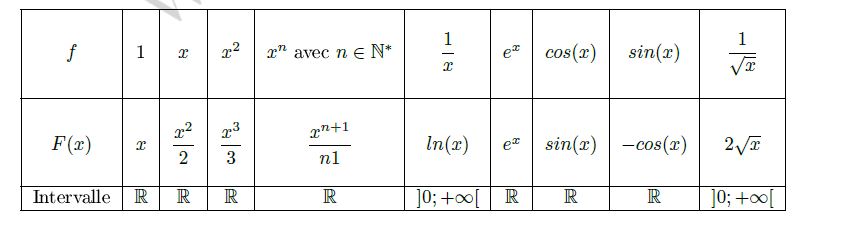$f$ est continue sur $\mathbb{R}$ donc sur $[0;ln(2)]$ et admet donc des primitives.
$F(x)=2e^x$ est une primitive de $f$ sur $\mathbb{R}$
En effet $F'(x)=2e^x=f(x)$
$F(0)=2e^0=2$ (rappel $e^0=1$)
$F(ln(2))=2e^{ln(2)}=2\times 2=4$
$\int_0^{ln(2)} 2e^{x} dx=F(2)-F(0)=4-2=2$ $\int_0^{ln(2)} 2e^{x} dx=2$

Si on pose $f(x)=e ^{2x}$ on a $f$ continue sur $\mathbb{R}$ donc $f$ admet des primitives sur $[0;1]$.
$F(x)=\dfrac{e^{2x}}{2}$ est une primitive de $f$ sur $\mathbb{R}$.
En effet $F'(x)=\dfrac{2e^{2x}}{2}=e^{2x}=f(x)$
$F(0)=\dfrac{e^{2\times 0}}{2}=\dfrac{e^0}{2}=\dfrac{1}{2}$
et $F(1)=\dfrac{e^{2\times 1}}{2}=\dfrac{e^2}{2}$
$\int_0^1 f(x)dx=[F(x)]_0^1=\dfrac{e^2}{2}-\dfrac{1}{2}=\dfrac{e^2-1}{2}$
$\int_0^1 e^{2x} dx=\dfrac{e^2-1}{2}$
Contrôle avec la calculatrice
Touches OPTION puis CALC puis $\int$ avec la syntaxe $\int$(fonction, borne inférieure, borne supérieure)
Avec une TI, la syntaxe est int(fonction, variable,borne inférieure, borne supérieure)

Si on pose $u(x)=4-2x$ on a $u'(x)=-2$
$f(x)=\dfrac{-1}{2}\times (-2)e^{4-2x}=\dfrac{-1}{2}u'(x)e^{u(x)}$
$f$ continue sur $\mathbb{R}$ donc $f$ admet des primitives sur $[0;2]$.
$F(x)=\dfrac{-1}{2}e^{4-2x}$ est une primitive de $f$ sur $[0;2]$.
En effet $F'(x)=\dfrac{-1}{2}\times (4-2x)e^{4-2x}=\dfrac{-1}{2}\times (-2)\times e^{4-2x}=e^{4-2x}=f(x)$
$F(0)=\dfrac{-1}{2}e^{4-2\times 0}=\dfrac{-e^4}{2}$
et $F(2)=\dfrac{-1}{2}e^{4-2\times 2}=\dfrac{-e^0}{2}=\dfrac{-1}{2}$ (rappel $e^0=1$)
$\int_{0}^2 f(x)dx=[F(x)]_{0}^2=F(2)-F(0)=\dfrac{-1}{2}-\dfrac{-e^4}{2}=\dfrac{e^4-1}{2}$
$\int_{0}^2 e^{4-2x} dx=\dfrac{e^4-1}{2}$
penser à contrôler avec la calculatrice