Dans le plan muni d'un repère orthogonal, on donne $A(-2;2)$, $B(2;3)$ et $C(3;-1)$.
- Calculer les coordonnées du vecteur $\overrightarrow{AB}$.
Coordonnées d'un vecteur défini par deux points
Si $A(x_A;y_A)$ et $B(x_B;y_B)$ alors $\overrightarrow{AB}(x_B-x_A;y_B-y_A)$ (coordonnées du second point $-$ coordonnées du premier point)$\begin{cases} x_{\overrightarrow{AB}}=x_B-x_A=2-(-2)=4\\ y_{\overrightarrow{AB}}=y_B-y_A=3-2=1 \end{cases}$
Contrôler le calcul sur le graphique en plaçant les points dans un repère. - Calculer les coordonnées du point $D$ tel que $\overrightarrow{CD}=2\overrightarrow{AB}$.
Coordonnées de la somme et du produit par un réel
Si $\overrightarrow{u}(x;y)$ et $\overrightarrow{w}(x';y')$ alors:
$\overrightarrow{u}=\overrightarrow{w} \Longleftrightarrow \begin{cases} x=x'\\ y=y' \end{cases}$
$\overrightarrow{u}+\overrightarrow{w}(x+x';y+y')$
$k\overrightarrow{u}(kx;ky)$Il faut calculer les coordonnées de $2\overrightarrow{AB}$
Les coordonnées de $2\overrightarrow{AB}$ et $\overrightarrow{CD}$ sont égales.On pose $D(x;y)$.
$\begin{cases} x_{\overrightarrow{CD}}=x_D-x_C=x-3\\ y_{\overrightarrow{CD}}=y_D-y_C=y-(-1)=y+1 \end{cases}$ donc $\overrightarrow{CD}(x-3;y+1)$
$\overrightarrow{CD}=2\overrightarrow{AB}$ donc on a:
$\begin{cases} x_{\overrightarrow{CD}}=2x_{\overrightarrow{AB}}\\ y_{\overrightarrow{CD}}=2y_{\overrightarrow{AB}} \end{cases} \Longleftrightarrow \begin{cases} x-3=2\times 4\\ y+1=2\times 1 \end{cases} $
$\phantom{\begin{cases} x_{\overrightarrow{CD}}=2x_{\overrightarrow{AB}}\\ y_{\overrightarrow{CD}}=2y_{\overrightarrow{AB}} \end{cases}} \Longleftrightarrow \begin{cases} x=11\\ y=1 \end{cases} $
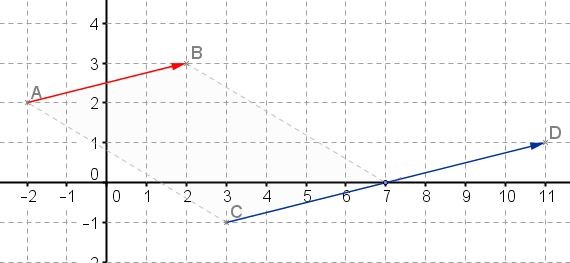
- Calculer les coordonnées du point $E$ image du point $D$ par la translation de vecteur $\overrightarrow{u}(1;-4)$.
On veut que les vecteurs $\overrightarrow{DE}$ et $\overrightarrow{u}$ soient égaux donc qu'ils aient les mêmes coordonnées.On pose $E(x;y)$.
$\begin{cases} x_{\overrightarrow{DE}}=x_E-x_D=x-11\\ y_{\overrightarrow{DE}}=y_E-y_C=y-1 \end{cases}$ donc $\overrightarrow{DE}(x-11;y-1)$
$E$ est l'image du point $D$ par la translation de vecteur $\overrightarrow{u}(1;-4)$.
donc $\overrightarrow{DE}=\overrightarrow{u}$
$\begin{cases} x_{\overrightarrow{DE}}=x_{\overrightarrow{u}}\\ y_{\overrightarrow{DE}}=y_{\overrightarrow{u}} \end{cases} \Longleftrightarrow \begin{cases} x-11=1\\ y-1=-4 \end{cases} $
$\phantom{\begin{cases} x_{\overrightarrow{DE}}=x_{\overrightarrow{u}}\\ y_{\overrightarrow{DE}}=y_{\overrightarrow{u}} \end{cases}} \Longleftrightarrow \begin{cases} x=12\\ y=-3 \end{cases} $
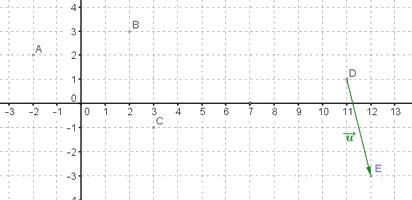
- Quelle est la nature du quadrilatère $BDEC$?
On veut que les vecteurs $\overrightarrow{BD}$ et $\overrightarrow{CE}$ soient égaux donc qu'ils aient les mêmes coordonnées.$\begin{cases} x_{\overrightarrow{BD}}=x_D-x_B=11-2=9\\ y_{\overrightarrow{BD}}=y_D-y_B=1-3=-2 \end{cases}$
donc $\overrightarrow{BD}(9;-2)$
$\begin{cases} x_{\overrightarrow{CE}}=x_E-x_C=12-3=9\\ y_{\overrightarrow{CE}}=y_E-y_C=-3-(-1)=-2 \end{cases}$
donc $\overrightarrow{CE}(9;-2)$
Les deux vecteurs ont des coordonnées égales
donc $\overrightarrow{BD}=\overrightarrow{CE}$
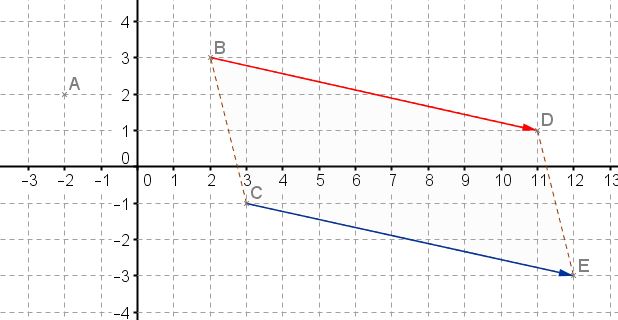
On peut aussi calculer les coordonnées du milieu $I$ de $[BE]$ et du milieu de $I'$ de $[CD]$ et vérifier que $I$ et $I'$ sont confondus.
Rappel sur les coordonnées du milieu $I$:
$\begin{cases} x_{I}=\dfrac{x_B+x_E}{2}=\dfrac{2+12}{2}=7\\ y_{I}=\dfrac{y_B+y_E}{2}=\dfrac{3-3}{2}=0 \end{cases}$
Attention les fonctions ci-dessous sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Cours nº 398
Vous pouvez retourner sur le cours après avoir vu cette vidéo.
Vecteurs et coordonnées
- coordonnées du milieu
- distances et norme d'un vecteur
- coordonnées de la somme et du produit par un réel
- déterminant de deux vecteurs et vecteurs colinéaires
- alignement de trois points dans un repère
infos cours
| 15-20mn
série 8 : Coordonnnées d'un vecteur, distances et milieu
exercices semblables
Si vous souhaitez vous emtraîner un peu plus, nous vous conseillons ces exercices.