L'espace est muni d'un repère $(O;\overrightarrow{i};\overrightarrow{j};\overrightarrow{k})$ et on donne les points $A(2;-3;1)$, $B(1;3;5)$ et $C(-1;3;-2)$.
- Calculer les coordonnées du vecteur $\overrightarrow{AB}$ puis du vecteur $\overrightarrow{AC}$.
Coordonnées d'un vecteur dans l'espace
L'espace est muni d'un repère quelconque.
Soit $A(x_A;y_A;z_A)$ et $B(x_B;y_B;z_B)$
$\overrightarrow{AB}\begin{pmatrix} x_B-x_A\\ y_B-y_A\\ z_B-z_A \end{pmatrix} $$\begin{cases} x_{\overrightarrow{AB}}=x_B-x_A=1-2=-1\\ y_{\overrightarrow{AB}}=y_B-y_A=3-(-3)=6\\ z_{\overrightarrow{AB}}=z_B-z_A=5-1=4 \end{cases}$
$\begin{cases} x_{\overrightarrow{AC}}=x_C-x_A=-1-2=-3\\ y_{\overrightarrow{AC}}=y_C-y_A=3-(-3)=6\\ z_{\overrightarrow{AC}}=z_C-z_A=-2-1=-3 \end{cases}$
- Vérifier que les points $A$, $B$ et $C$ ne sont pas alignés.
$A$, $B$ et $C$ sont alignés si et seulement si les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$ sont colinéaires.$x_{\overrightarrow{AC}}=-3=3x_{\overrightarrow{AB}}$
et $y_{\overrightarrow{AC}}=6=y_{\overrightarrow{AB}}$
donc il n'existe pas de réel $k$ tel que $\overrightarrow{AC}=k\overrightarrow{AB}$
donc les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$ ne sont pas colinéaires
- Déterminer les coordonnées du point $M$ défini par la relation $\overrightarrow{AM}=2\overrightarrow{AB}-3\overrightarrow{AC}$
On a donc $x_{\overrightarrow{AM}}=2x_{\overrightarrow{AB}}-3x_{\overrightarrow{AC}}$$\overrightarrow{AM}=2\overrightarrow{AB}-3\overrightarrow{AC}$
donc on a les équations suivantes:
$\begin{cases} x_M-x_A=2x_{\overrightarrow{AB}}-3x_{\overrightarrow{AC}}\\ y_M-y_A=2z_{\overrightarrow{AB}}-3y_{\overrightarrow{AC}}\\ z_M-z_A=2z_{\overrightarrow{AB}}-3z_{\overrightarrow{AC}} \end{cases}$
$ \Longleftrightarrow \begin{cases} x_M-2=2\times (-1)-3\times (-3)\\ y_M-(-3)=2\times 6-3\times 6\\ z_M-1=2\times 4-3\times (-3) \end{cases}$
$ \Longleftrightarrow \begin{cases} x_M=9\\ y_M=-9\\ z_M=18 \end{cases}$
- Que peut-on en déduire pour les points $A$, $B$, $C$ et $M$?
vecteurs coplanaires
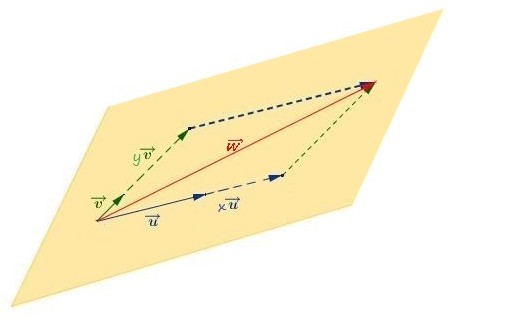
Trois vecteurs $\overrightarrow{u}$, $\overrightarrow{v}$ et $\overrightarrow{w}$ non nuls sont coplanaires si les points $A$, $B$, $C$ et $D$ définis par $\overrightarrow{AB}=\overrightarrow{u}$, $\overrightarrow{AC}=\overrightarrow{v}$ et $\overrightarrow{AD} =\overrightarrow{w}$ sont dans un même plan.
 $\overrightarrow{AM}=2\overrightarrow{AB}-3\overrightarrow{AC}$
$\overrightarrow{AM}=2\overrightarrow{AB}-3\overrightarrow{AC}$
- On donne $N(5;y;z)$, déterminer les coordonnées de $N$ pour que $A$, $B$ et $N$ soient alignés.
Il faut que les vecteurs $\overrightarrow{AN}$ et $\overrightarrow{AB}$ soient colinéaires.$A$, $B$ et $N$ sont alignés si et seulement si les vecteurs $\overrightarrow{AN}$ et $\overrightarrow{AB}$ soient colinéaires.
donc il existe un réel $k$ tel que $\overrightarrow{AN}=k\overrightarrow{AB}$
On a $x_{\overrightarrow{AN}}=x_N-x_A=5-2=3$ et $x_{\overrightarrow{AB}}=-1$
donc $3=k\times (-1)$ soit $k=-3$
On a alors $\overrightarrow{AN}=-3\overrightarrow{AB}$
$\begin{cases} y_N-y_A=-3y_{\overrightarrow{AB}}\\ z_N-z_A=-3z_{\overrightarrow{AB}} \end{cases} \Longleftrightarrow \begin{cases} y_N-(-3)=-3\times 6\\ z_N-1=-3\times 4 \end{cases} $
$\phantom{\begin{cases} y_N-y_A=-3y_{\overrightarrow{AB}}\\ z_N-z_A=-3z_{\overrightarrow{AB}} \end{cases} } \Longleftrightarrow \begin{cases} y_N=-21\\ z_N=-11 \end{cases} $
Attention les fonctions ci-dessous sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Cours nº 1391
Vous pouvez retourner sur le cours après avoir vu cette vidéo.
Coordonnées dans l'espace
- coordonnées d'un vecteur défini par deux points
- vecteurs colinéaires
- coordonnées du milieu et calcul de distances
infos cours
| 15mn
série 2 : Coordonnées d'un point et d'un vecteur, distances
exercices semblables
Si vous souhaitez vous emtraîner un peu plus, nous vous conseillons ces exercices.