La fonction $f$ est définie sur $\mathbb{R}$ et pour tout réel $x $ on a $2x-1 \leq f(x) \leq 2x+1$
- Déterminer $\displaystyle \lim_{x \rightarrow +\infty}f(x)$ et déterminer $\displaystyle \lim_{x \rightarrow -\infty}f(x)$
Limite par comparaison
Soit $f$ et $g$ définie sur $I=]a;+\infty[$ telles que $f(x)\leq g(x)$ sur $I$.
Si $\displaystyle \lim_{x \rightarrow +\infty}f(x)=+\infty$ alors $\displaystyle \lim_{x \rightarrow +\infty}g(x)=+\infty$
Si $\displaystyle \lim_{x \rightarrow +\infty}g(x)=-\infty$ alors $\displaystyle \lim_{x \rightarrow +\infty}f(x)=-\infty$il faut chercher la limite de $2x-1$ et de $2x+1$$\displaystyle \lim_{x \rightarrow +\infty}2x-1=+\infty$
et pour tout réel $x$ on a $f(x)\geq 2x-1$
$\displaystyle \lim_{x \rightarrow -\infty}2x+1=-\infty$
et pour tout réel $x$ on a $f(x)\leq 2x+1$
- La fonction $g$ est définie sur $\mathbb{R}$ par $g(x)=2x+cos(x)$.
Montrer que pour tout réel $x$ on a $2x-1 \leq g(x)\leq 2x+1$ et en déduire les limites de $g$ en $+\infty$ et $-\infty$.Limite par comparaison
Soit $f$ et $g$ définie sur $I=]a;+\infty[$ telles que $f(x)\leq g(x)$ sur $I$.
Si $\displaystyle \lim_{x \rightarrow +\infty}f(x)=+\infty$ alors $\displaystyle \lim_{x \rightarrow +\infty}g(x)=+\infty$
Si $\displaystyle \lim_{x \rightarrow +\infty}g(x)=-\infty$ alors $\displaystyle \lim_{x \rightarrow +\infty}f(x)=-\infty$Rappel: $-1 \leq cos(x) \leq 1$Pour tout réel $x$, on a $-1 \leq cos(x)\leq 1$
donc $2x-1\leq 2x+cos(x)\leq 2x+1$ (on ajoute $2x$ à chacun des membres de l'inégalité)
soit $2x-1 \leq g(x)\leq 2x+1$
En utilisant les résultats de la question 1, on peut en déduire que
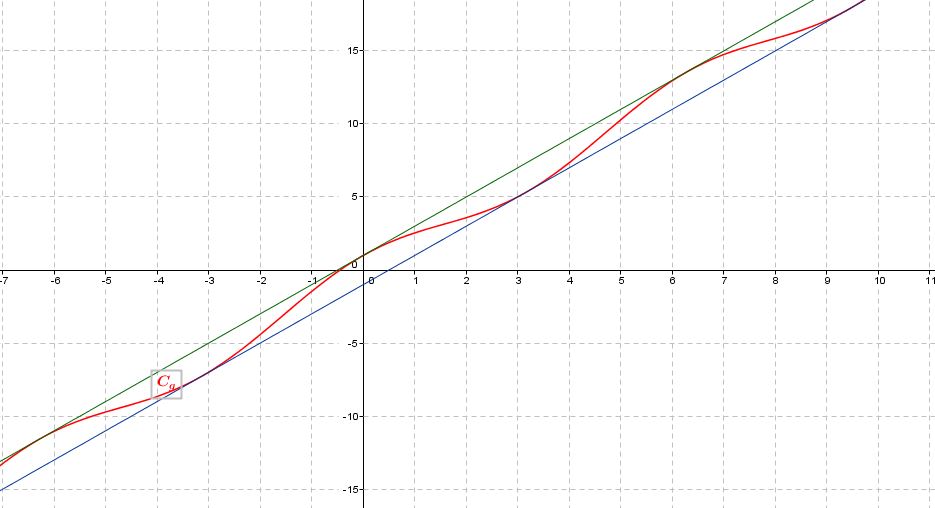
- Représenter graphiquement la fonction $g$ et les droites d'équations $y=2x-1$ et $y=2x+1$ sur la calculatrice ou avec un logiciel.
On peut utiliser le MENU TABLE de la calculatrice en saisissant $f(x)$ dans Y1, et les équations des deux droites dans Y2 et Y3.On peut utiliser le MENU TABLE de la calculatrice en saisissant $f(x)$ dans Y1, et les équations des deux droites dans Y2 et Y3
Penser à ajuster les unités du repère (SHIFT F3 (V-Window))
Avec GEOGEBRA, on obtient:
Attention les fonctions ci-dessous sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Cours nº 1105
Vous pouvez retourner sur le cours après avoir vu cette vidéo.
Limites par comparaison et encadrement
- limite par comparaison
- limite par encadrement (théorème des gendarmes)
infos cours
| 10-12mn
série 5 : Limites par comparaison