1. spécialité maths première
  2. chapitre
  3. devoir corrigé nº665
PDF reservé aux abonnés
Exercice 1 (4 points)
Résoudre
  1. $\dfrac{2x^2-10x-5}{x+2} = x-3$

    Rappel de cours

    Racines

    Les racines de $p(x)=ax^2+bx+c$ avec$a\neq 0$ sont les valeurs de $x$ annulant $P$
    c'est à dire telles que $P(x)=0$.
    $\Delta=b^2-4ac$
    Si $\Delta>0$ donc il y a deux racine $x_1=\dfrac{-b+\sqrt{\Delta}}{2a}$ et $x_2=\dfrac{-b-\sqrt{\Delta}}{2a}$
    Si $\Delta=0$ il y a une racine (double) $x_1=\dfrac{-b}{2a}$
    Si $\Delta<0$ il n'y a aucune racine
    Remarque: Graphiquement, les racines sont les abscisses des points d'intersection de la parabole et de l'axe des abscisses.

    Aide

    rechercher d'abord la valeur interdite
    Les produits en croix sont égaux
    Il faut se ramener à une équation de la forme $ax^2+bx+c=0$

    Solution

    - Recherche de $D_f$
    Il faut $x+2\neq 0$ soit $x\neq -2$
    On résout sur $D_f=\mathbb{R} \setminus \left\lbrace -2 \right\rbrace $
    - Pour tout réel $x \in D_f$:
    $\dfrac{2x^2-10x-5}{x+2} = x-3$
    $\Longleftrightarrow 2x^2-10x-5=(x+2)(x-3)$
    $\Longleftrightarrow 2x^2-10x-5=x^2-x-6$
    $\Longleftrightarrow x^2-9x+1=0$
    - $\Delta=b^2-4ac=81-4=77$
    $\Delta>0$ donc il y a deux racines:
    $x_1=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{9-\sqrt{77}}{2}$
    et $x_2=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{9+\sqrt{77}}{2}$
    $x_1 \in D_f$ et $x_2\in D_f$
  2. $x^4-6x^2+8=0$

    Aide

    On peut poser $X=x^2$

    Solution

    On pose $X=x^2$
    et il faut alors résoudre l'équation $X^2-6X+8=0$
    $\Delta=b^2-4ac=36-32=4$
    $\Delta>0$ donc il y a deux racines:
    $X_1=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{6-2}{2}=2$
    et $X_2=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{6+2}{2}=4$
    On doit résoudre:
    $x^2=2$ ou $x^2=4$
    $\Longleftrightarrow x=\sqrt{2}$ ou $x=-\sqrt{2}$ ou $x=2$ ou $x=-2$
  3. $1020x^2+x-1021=0$

    Rappel de cours

    Somme et produit des racines

    Si le polynôme $P(x)=ax^2+bx+c$ (avec $a\neq 0$) admet deux racines $x_1$ et $x_2$ alors on a:
    $ x_1+x_2=\dfrac{-b}{a}$ (somme des racines)
    et $x_1x_2=\dfrac{c}{a}$ (produit des racines)

    Aide

    On peut remarquer que 1 est une racine du polynôme

    Solution

    On peut remarquer que $1020+1-1021=0$ donc $x_1=1$ est une solution.
    On a $x_1x_2=\dfrac{c}{a}$ soit $x_2=\dfrac{-1021}{1020}$.
Exercice 2 (5 points)
Résoudre
  1. $-2x^2+5x-3>0$

    Rappel de cours

    Signe de $ax^2+bx+c$

    - Cas $\Delta>0$ (deux racines $x_1$ et $x_2$

    - Cas $\Delta=0$ (une racine $x_1$)

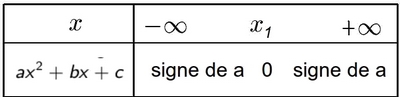
    - Cas $\Delta<0$ (aucune racine)

    Solution

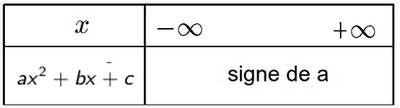    -Recherche des racines de $-2x^2+5x-3$
    $-2+5-3=0$ donc $x_1=1$ est une racine.
    $x_1x_2=\dfrac{c}{a} \Longleftrightarrow x_2=\dfrac{3}{2}$
    - Signe de $-2x^2+5x-3$

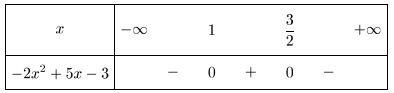
  2. $ \frac{2x^2-5x+1}{3-x}\leqslant 2$

    Aide

    il faut chercher les valeurs interdites
    puis passer se ramener à une étude de signe du quotient en passant 2 à gauche

    Solution

    - Il faut $3-x\neq 0$ soit $x \neq 3$
    donc $D_f=\mathbb{R} \setminus\left\lbrace 3 \right\rbrace $
    - Pour tout réel $x\in D_f$:
    $\dfrac{2x^2-5x+1}{3-x}\leqslant 2$
    $\Longleftrightarrow \dfrac{2x^2-5x+1}{3-x}-2\leqslant 0$
    $\Longleftrightarrow \dfrac{2x^2-5x+1-2(3-x)}{3-x}\leqslant 0$
    $\Longleftrightarrow \dfrac{2x^2-5x+1-6+2x)}{3-x}\leqslant 0$
    $\Longleftrightarrow \dfrac{2x^2-3x-5}{3-x}\leqslant 0$
    - Racines de $2x^2-3x-5$
    $\Delta=b^2-4ac=9+40=49$
    $\Delta>0$ donc il y a deux racines:
    $x_1=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{3-7}{4}=-1$
    et
    $x_2=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{3+7}{4}=\dfrac{5}{2}$
    - Tableau de signes

Exercice 3 (4 points)
Soit $P$ le polynôme défini sur $\mathbb{R}$ par : $P(x)=x^3-4x^2+5x-2$. On veut résoudre $P(x)=0$.
  1. Montrer que 2 est une solution de cette équation.

    Aide

    Il faut vérifier que $P(2)=0$

    Solution

    $P(2)=2^3-4\times 2^2+5\times 2-2=8-16+10-2=0$
  2. Déterminer alors les réels $a$, $b$ et $c$ tels que : $P(x)=(x-2)(ax^2+bx+c)$.

    Aide

    Il faut développer $P(x)=(x-2)(ax^2+bx+c)$ et identifier les coefficients

    Solution

    Pour tout réel $x$:
    $P(x)=(x-2)(ax^2+bx+c)$
    $=ax^3+bx^2+cx-2ax^2-2bx-2c$
    $=ax^3+bx^2-2ax^2+cx-2bx-2c$
    $=x^3-4x^2+3x+2$
    Par identification des coefficients:
    $a=1$
    $b-2a=-4 \Longleftrightarrow b=-4+2a=-2$
    $c-2b=5 \Longleftrightarrow c=5+2b=1$
    et on a bien $-2c=-2$
  3. En déduire les solutions de l'équation $P(x)=0$.

    Rappel de cours

    Racines

    Les racines de $p(x)=ax^2+bx+c$ avec$a\neq 0$ sont les valeurs de $x$ annulant $P$
    c'est à dire telles que $P(x)=0$.
    $\Delta=b^2-4ac$
    Si $\Delta>0$ donc il y a deux racine $x_1=\dfrac{-b+\sqrt{\Delta}}{2a}$ et $x_2=\dfrac{-b-\sqrt{\Delta}}{2a}$
    Si $\Delta=0$ il y a une racine (double) $x_1=\dfrac{-b}{2a}$
    Si $\Delta<0$ il n'y a aucune racine
    Remarque: Graphiquement, les racines sont les abscisses des points d'intersection de la parabole et de l'axe des abscisses.

    Aide

    Il faut chercher les racines du facteur de degré 2

    Solution

    $P(x)=0 \Longleftrightarrow x-2=0$ ou $x^2-2x-1=0$
    $\phantom{P(x)=0} \Longleftrightarrow x-2=0$ ou $(x-1)^2=0$
    $\phantom{P(x)=0} \Longleftrightarrow x-2=0$ ou $x=1$
Exercice 4 (4 points)
  1. Résoudre l'inéquation $m^2+5m+4>0$ d'inconnue $m$.

    Rappel de cours

    Signe de $ax^2+bx+c$

    - Cas $\Delta>0$ (deux racines $x_1$ et $x_2$

    - Cas $\Delta=0$ (une racine $x_1$)

    - Cas $\Delta<0$ (aucune racine)

    Solution

    Racines de $m^2+5m+4$:
    $\Delta=5^2-4\times 1\times 4=9$
    $\Delta>0$ donc il y a deux racines
    $x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{ -5+3}{ 2 }=-1$
    et $x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-5 -3 }{2 }=-4$

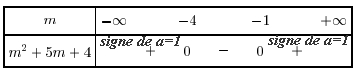
  2. En déduire les valeurs de $m$ pour lesquelles l'équation $4mx^2+4(m+2)x-1=0$ admet deux solutions distinctes.

    Aide

    Il faut que le discriminant soit strictement positif

    Solution

    $\Delta_1=\left(4(m+2)\right)^2-4\times 4m\times (-1)$
    $\phantom{\Delta_1}=16(m+2)^2+16m$
    $\phantom{\Delta_1}=16(m^2+4m+4)+16m$
    $\phantom{\Delta_1}=16m^2+64m+64+16m$
    $\phantom{\Delta_1}=16m^2+80m+64$
    $\phantom{\Delta_1}=16(m^2+5m+4)$
    Il y a deux solutions si $\Delta >0$ donc si $m^2+5m+4>0$ (inéquation de la question 1)
Exercice 5 (3 points)
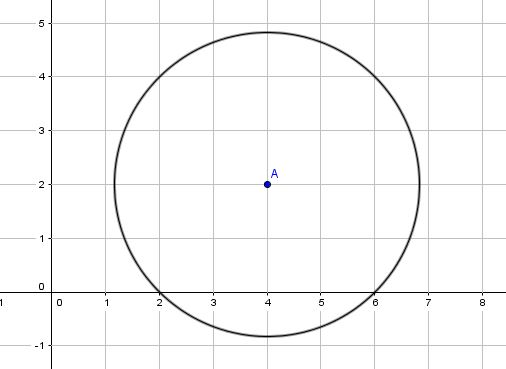
On considère un repère orthonormé et le cercle $\mathcal{C}$ de centre $A(4;2)$ et de rayon $2\sqrt{2}$ unités.
On rappelle que dans un repère orthonormé, $AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}$ avec $A(x_A;y;A)$ et $B(x_B;y_B)$.
  1. Montrer que les coordonnées d'un points $M(x;y)$ appartenant au cercle $\mathcal{C}$ doivent vérifier l'égalité $x^2-8x+y^2-4y+12=0$.

    Rappel de cours

    include65 fclude

    Solution

    $M \in \mathcal{C} \Longleftrightarrow AM=2 \Longleftrightarrow AM^2=(2\sqrt{2})^2=8$
    $AM^2=(x-4)^2+(y-2)^2$
    $\phantom{AM^2}=x^2-8x+16+y^2-4y+4$
    $\phantom{AM^2}=x^2-8x+y^2-4y+20$
    $AM^2=8 \Longleftrightarrow x^2-8x+y^2-4y+20=8 \Longleftrightarrow x^2-8x+y^2-4y+12=0$
  2. En déduire les coordonnées des points d'intersection du cercle $\mathcal{C}$ avec les axes du repères (axe des abscisses et axe des ordonnées).
    On pourra faire une figure pour contrôler graphiquement les résultats obtenus.

    Aide

    Il faut avoir $x=0$ puis $y=0$

    Solution

    Avec l'axe des abscisses:
    On a alors $y_M=y=0$ et donc $x^2-8x+12=0$
    $2^2-8\times 2+12=4-16+12=0$
    donc $x_1=2$ est une solution et $x_1x_2=\dfrac{c}{a}$
    soit $2x_2=12$ donc $x_2=6$

    Avec l'axe des ordonnées:
    On a alors $x_M=y=0$ et donc $y^2-4y+5=0$
    $\Delta=b^2-4ac=(-4)^2-4\times 1\times 5=16-20=-4$
    donc il n'y a aucune solution
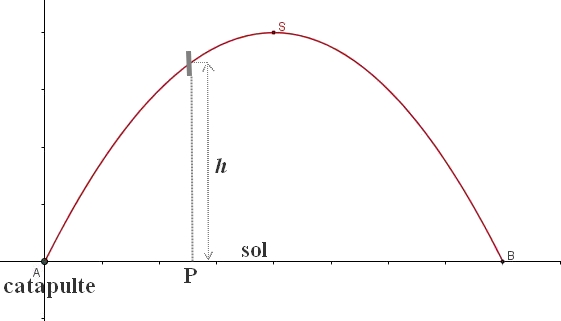
\ex{3} Dans une foire, une catapulte permet de lancer des billes sur une cible. La trajectoire de ces billes et un arc de parabole(voir schéma ci-dessous) où $A$ est le point de lancement et $S$ le sommet de l'arc de parabole.

Lors de son lancer, Pierre envoie la bille pour laquelle la hauteur maximale atteinte est de 4,9 m et retombant sur le sol à 14 mètres du point de lancement.
On place une cible circulaire de diamètre 25cm à 10 mètres de la catapulte(point P) dont le centre est à une hauteur $h=3,9$ mètres.
La bille de Pierre traversera-t-elle la cible?

Solution

On considère le repère orthonormé d'unité 1m et d'origine $A$.
On note $P$ la fonction dont la représentation graphique est la parabole correspondant à la trajectoire de la bille.
Les racines de $P$ sont $x_1=0$ et $x_2=14$.
Le sommet $S$ a pour ordonnée $y_S=4,9$ et pour abscisse $x_S=\dfrac{0+14}{2}=7$ (milieu de $[AB ]$).
On a donc $P(x)=a(x-7)^2+4,9$.
$P(0)=0 \Longleftrightarrow a(0-7)^2+4,9=0 \Longleftrightarrow a=\dfrac{-4,9}{49}=-0,1$
donc $P(x)=-0,1(x-7)^2+4,9$
Lorsque la bille passera au niveau de la cible, on aura alors pour abscisse 10 et la bille sera a une hauteur de $P(10)=-0,1(10-7)^2+4,9=4$ mètres.
La cible a un diamètre de 25cm soit un rayon de 12,5cm=0,125m.
Le bas de la cible est donc a une hauteur de $h_1=3,9-0,125=3,775$m et le haut de la cible a une hauteur de $h_2=3,9+0,125=4,025$
On a bien $P(10)$ compris entre $h_1$ et $h_2$

exercices semblables


Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
réf 612: Équation avec des quotients menant au second degré
| 6-8mn |
réf 654: Équation avec un paramètre
| 8-10mn |
réf 618: Inéquations avec un quotient
| 8-12mn |