Exercice 1 (3 points)
Pour chaque polynôme, dresser le tableau de variation .
- $P(x)=2x^2-4x-1$
Forme canonique
Toute fonction polynôme de degré 2 définie sur $\mathbb{R}$ par $P (x) = ax^2 + bx + c$ peut s'écrire sous la forme $P (x) = a(x -\alpha)^2 + \beta$ avec $\alpha=\dfrac{-b}{2a}$ et $\beta= P ( \alpha)$.
Cette écriture de $P (x)$ est appelée forme canonique et $S(\alpha;\beta)$ est le sommet de la parabole représentant la fonction $P$Variations fonction polynôme du second degré
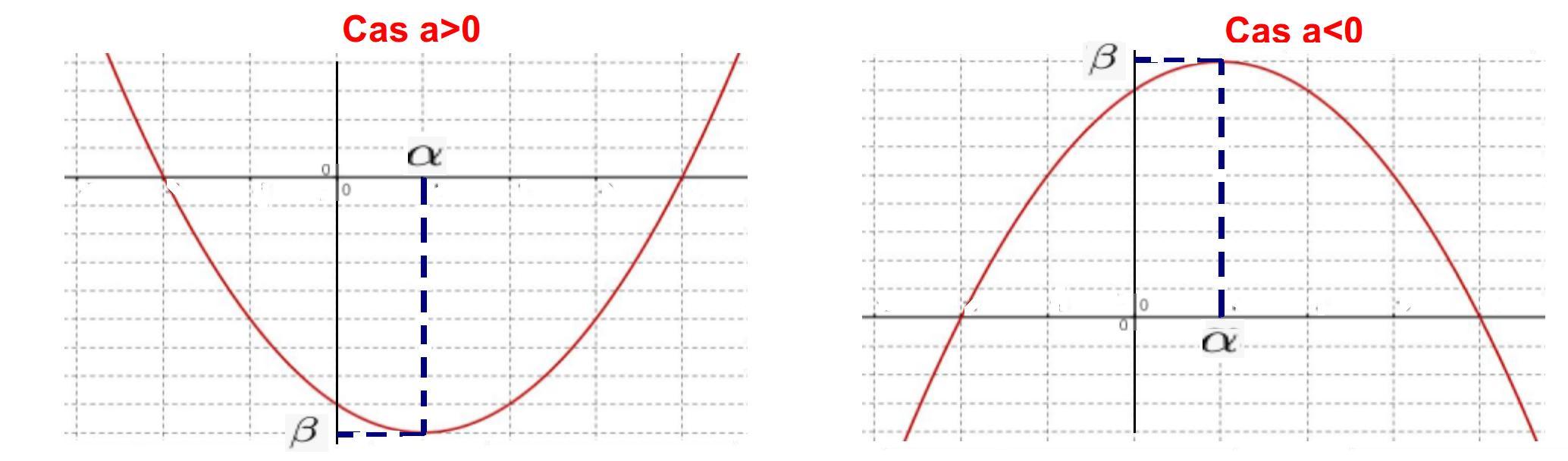
Soit la fonction $P$ définie sur $\mathbb{R}$ par sa forme canonique $P (x) = a(x-\alpha)^2 + \beta$
La courbe représentative de $P$ est une parabole dont le sommet a pour coordonnées $(\alpha; \beta)$.
Tableau de variation: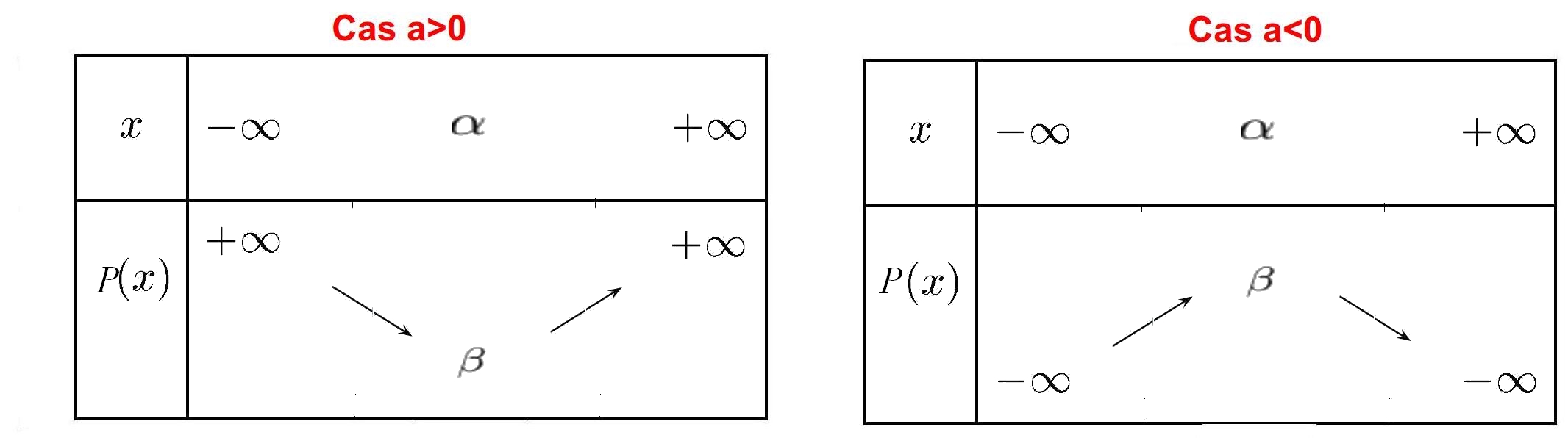
 Calculer $\alpha$ et $f(\alpha)$On a $a=2$, $b=-4$ et $c=-1$
Calculer $\alpha$ et $f(\alpha)$On a $a=2$, $b=-4$ et $c=-1$
$\alpha=\dfrac{-b}{2a}=\dfrac{4}{4}=1$
$\beta=f(\alpha)=f(1)=2\times 1^2-4\times 1 -1=2-4-1=-3$
donc $P(x)=a(x-\alpha)^2+\beta=2(x-1)^2-3$
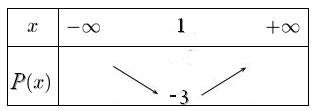
Le coefficient $a$ de $x^2$ est positif donc on a:
- $P(x)=3+x^2+2x$
écrire le polynôme en ordonnant selon les puissances décroissantes de $x$$P(x)=3+x^2+2x=x^2+2x+3$
$a=1$, $b=2$ et $c=3$
$\alpha=\dfrac{-b}{2a}=\dfrac{-2}{2}=-1$
$\beta=f(\alpha)=f(-1)= (-1)^2+2\times (-1)+3=1-2+3=2$
donc $P(x)=a(x-\alpha)^2+\beta=(x-(-1))^2+2=(x+1)^2+2$
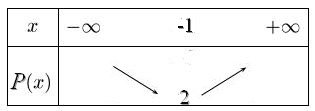
Le coefficient $a$ de $x^2$ est positif donc on a:
Exercice 2 (4 points)
Résoudre dans $\mathbb{R}$
- $2x^2-8x-24=0$
Discriminant
$P(x)=ax^2+bx+c$ avec $a\neq 0$.
Le discriminant du polynôme du second degré $P$ est $\Delta=b^2-4ac$Calculer le discriminant $\Delta$$\Delta=b^2-4ac=(-8)^2-4\times 2\times (-24)=64+192=256$
$\Delta>0$ donc il y a deux solutions:
$x_1=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{8-16}{4}=6-2$ et $x_2=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{8+16}{4}=6$
Penser à contrôler les solutions avec la calculatrice (MENU EQUA) - $(2x-1)(x-3)=4x-9$
Développer, simplifier et se ramener +a une équation de la forme $ax^2+bx+c=0$$(2x-1)(x-3)=4x-9\Longleftrightarrow 2x^2-6x-x+3-(4x-9)=0$
$\phantom{(2x-1)(x-3)=4x-9}\Longleftrightarrow 2x^2-7x+3-4x+9=0$
$\phantom{(2x-1)(x-3)=4x-9}\Longleftrightarrow 2x^2-11x+12=0$
$\Delta=b^2-4ac=(-11)^2-4\times 2 \times 12=25 $
$\Delta>0$
$x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{ 11+5 }{4}=4$
$x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{11-5 }{4}=\dfrac{3}{2}$
Exercice 3 (3 points)
Problème ouvert: Toute trace de recherche, même incomplète, sera valorisée dans la notation
Une entreprise vend des paquets de biscuits et le bénéfice journalier de cette entreprise, en euros, est donné par la fonction $B$ définie sur $[0;300]$ par $B(x)=-x^2+103x+100$ où $x$ est la quantité de paquets produite, exprimée en centaines de paquets.
Déterminer le nombre de paquets à produire chaque jour pour que le bénéfice soit maximum et le montant des bénéfices correspondant à cette quantité.
Forme canonique
Toute fonction polynôme de degré 2 définie sur $\mathbb{R}$ par $P (x) = ax^2 + bx + c$ peut s'écrire sous la forme $P (x) = a(x -\alpha)^2 + \beta$ avec $\alpha=\dfrac{-b}{2a}$ et $\beta= P ( \alpha)$.
Cette écriture de $P (x)$ est appelée forme canonique et $S(\alpha;\beta)$ est le sommet de la parabole représentant la fonction $P$
Variations fonction polynôme du second degré
Soit la fonction $P$ définie sur $\mathbb{R}$ par sa forme canonique $P (x) = a(x-\alpha)^2 + \beta$
La courbe représentative de $P$ est une parabole dont le sommet a pour coordonnées $(\alpha; \beta)$.
Tableau de variation:


Il faut déterminer la forme canonique de $B(x)$ et dresser sson tableau de variation
$\alpha=\dfrac{-b}{2a}=\dfrac{-103}{-2}=51,5$
$\beta=B(\alpha)=B(51,5)=-51,5^2+103\times 51,5+100=2752,25$
donc $B(x)=-(x-51,5)^2+2752,25$
Le coefficient $a$ de $x^2$ est négatif donc on a:
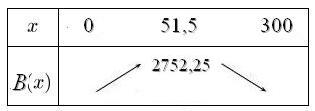
donc le maximum de $B$ est 2752,25 atteint en $x=51,5$.
Le nombre de paquets est donné en dizaines donc il faudra produire $51,5\times 100=5150$ paquets par jour.
$\beta=B(\alpha)=B(51,5)=-51,5^2+103\times 51,5+100=2752,25$
donc $B(x)=-(x-51,5)^2+2752,25$
Le coefficient $a$ de $x^2$ est négatif donc on a:

donc le maximum de $B$ est 2752,25 atteint en $x=51,5$.
Le nombre de paquets est donné en dizaines donc il faudra produire $51,5\times 100=5150$ paquets par jour.
vidéos semblables
Pour compléter ce devoir, nous vous conseillons les vidéos suivantes pour préparer ce devoir.
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.