MATHS-LYCEE
Exercice 1 (6 points)
On donne ci-dessous la représentation graphique $C_f$ de la fonction $f$ définie sur $\mathbb{R}\setminus \lbrace 3 \rbrace$.
Les droites $d$ et $d'$ sont asymptotes à la courbe $C_f$.
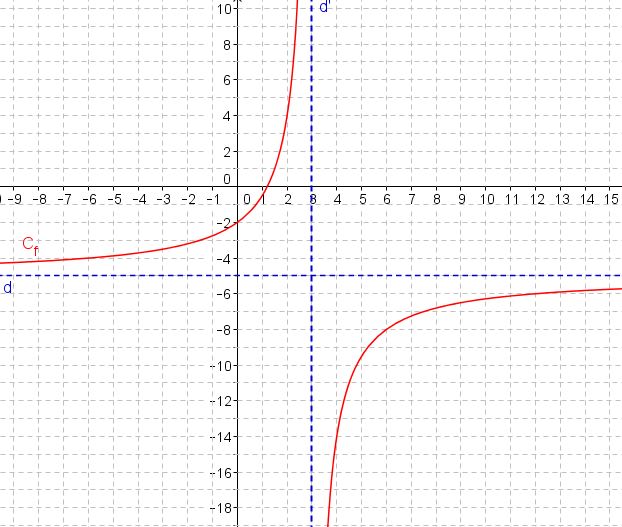
- Quelles sont les limites de $f$ en $+\infty$ et $-\infty$ et en $x=3$?
limite $l$ en $+\infty$ et interprétation graphique
La fonction $f$ est définie sur un intervalle $[a;+\infty[$ et $\ell \in \mathbb{R}$.
$\displaystyle \lim_{x \rightarrow +\infty}f(x)=\ell$ si pour tout intervalle ouvert I contenant $\ell$, il existe $x_0$ tel que pour tout $x>x_0$ on a $f(x)\in $ I
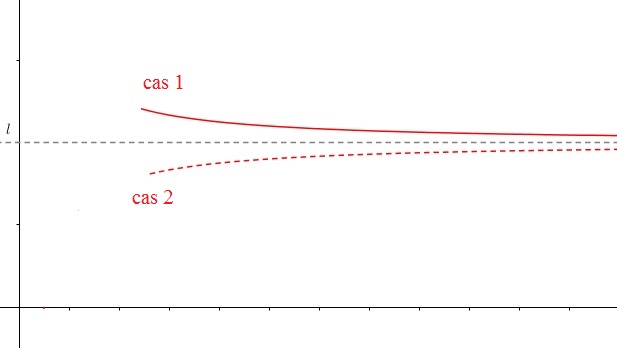
La droite d'équation $y=\ell$ est asymptote à la courbe en $+\infty$Limite infinie quand $x \longrightarrow a$
$f$ est définie sur un intervalle $I$ contenant $a$.
$\displaystyle \lim_{x \rightarrow a}f(x)=+\infty$ si pour tout réel $A>0$, il existe un réel $\epsilon>0$ avec $]a-\epsilon;a+\epsilon[\subset I$ tel que $f(x)>A$ pour tout $x\in ]a-\epsilon;a+\epsilon[$.
La droite d'équation $x=a$ est asymptote à a courbe.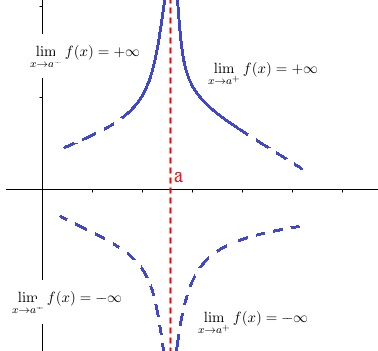
Pour les limites en $+\infty$ et $-\infty$, il faut utiliser l'asymptote $d$.
Pour les limites en $x=3$, il faut distinguer $x<3$ et $x>3$.La droite d'équation $y=-5$ est asymptote à la courbe en $+\infty$ et en $-\infty$
La droite d'équation $x=$ est asymptote à $C_f$
- On a $f(x)=\dfrac{6-5x}{x-3}$.
Retrouver les limites données par lecture graphique en $+\infty$ et $-\infty$Opérations sur les limites
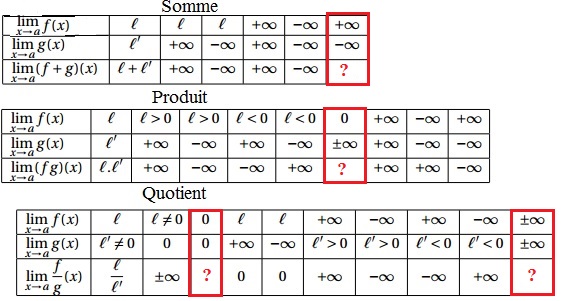Il faut factoriser $x$ au numérateur et au dénominateur.Pour tout réel $x\neq 0$, on a:
$f(x)=\dfrac{6-5x}{x-3}=\dfrac{x\left(\dfrac{6}{x}-5\right)}{x\left(x-\dfrac{3}{x}\right)}=\dfrac{\dfrac{6}{x}-5}{1-\dfrac{3}{x}}$
$\displaystyle \lim_{x \rightarrow -\infty} \dfrac{6}{x}-5=-5$ et $\displaystyle \lim_{x \rightarrow -\infty} 1-\dfrac{3}{x}=1$
$\displaystyle \lim_{x \rightarrow +\infty} \dfrac{6}{x}-5=-5$ et $\displaystyle \lim_{x \rightarrow +\infty} 1-\dfrac{3}{x}=1$
- Retrouver les limites de $f$ quand $x=3$.
Limite infinie quand $x \longrightarrow a$
$f$ est définie sur un intervalle $I$ contenant $a$.
$\displaystyle \lim_{x \rightarrow a}f(x)=+\infty$ si pour tout réel $A>0$, il existe un réel $\epsilon>0$ avec $]a-\epsilon;a+\epsilon[\subset I$ tel que $f(x)>A$ pour tout $x\in ]a-\epsilon;a+\epsilon[$.
La droite d'équation $x=a$ est asymptote à a courbe.
Il chercher la limite au numérateur et au dénominateur en distinguant les cas $x<3$ et $x>3$$\displaystyle \lim_{x \rightarrow 3}6-5x=6-5\times 3=-9$
Limite quand $x\longrightarrow 3^-$
$\displaystyle \lim_{x \rightarrow 3^-} x-3=0^-$ car $x-3 < 0$ pour $x<3$
Limite quand $x\longrightarrow 3^+$
$\displaystyle \lim_{x \rightarrow 3^+} x-3=0^+$ car $x-3 > 0$ pour $x>3$
Exercice 2 (8 points)
Déterminer les limites suivantes:
- $\displaystyle \lim_{x \rightarrow +\infty} \dfrac{x^2+3}{x-1}$.
Il faut factoriser le terme de plus haut degré au numérateur et au dénominateurPour tout réel $x\neq 0$, on a:
$\dfrac{x^2+3}{x-1}=\dfrac{x^2\left(1+\dfrac{3}{x^2}\right)}{x\left(1-\dfrac{1}{x}\right)}=\dfrac{x\left(1+\dfrac{3}{x^2}\right)}{1-\dfrac{1}{x}}$
$\displaystyle \lim_{x \rightarrow +\infty}1+\dfrac{3}{x^2}=1$ et $\displaystyle \lim_{x \rightarrow +\infty}x=+\infty$
donc par quotient $\displaystyle \lim_{x \rightarrow +\infty}x\left(1+\dfrac{3}{x^2}\right)=+\infty$
$\displaystyle \lim_{x \rightarrow +\infty} 1-\dfrac{1}{x}=1$
- $\displaystyle \lim_{x \rightarrow +\infty} \sqrt{\dfrac{2}{x^2+2}}$
Il faut chercher la limite de la composée en posant $u(x)=\dfrac{2}{x^2+2}$ et $v(x)=\sqrt{x}$$\displaystyle \lim_{x \rightarrow +\infty} x^2+2=+\infty$
$\displaystyle \lim_{x \rightarrow +\infty} \dfrac{2}{x^2+2}=0^+$
et $\displaystyle \lim_{x \rightarrow 0^+} \sqrt{\dfrac{2}{x^2+2}}=0$
- $\displaystyle \lim_{x \rightarrow +\infty} \dfrac{cos(x)}{x}$
Encadrement (théorème des "gendarmes")
$f$, $g$ et $h$ sont définies sur $I=]a;+\infty[$ telles que $f(x)\leq g(x)\leq h(x)$ sur $I$.
Si $\displaystyle \lim_{x \rightarrow +\infty}f(x)=\displaystyle \lim_{x \rightarrow +\infty}h(x)=l$ alors $\displaystyle \lim_{x \rightarrow +\infty}g(x)=l$ coursIl faut encadrer $\dfrac{cos(x)}{x}$Pour tout réel $x$, on a $-1\leq cos(x) \leq 1$
donc pour tout réel $x >0$, on a $\dfrac{-1}{x}\leq \dfrac{cos(x)}{x}\leq \dfrac{1}{x}$
$\displaystyle \lim_{x \rightarrow +\infty} \dfrac{-1}{x}= \displaystyle \lim_{x \rightarrow +\infty} \dfrac{1}{x}=0$
- $\displaystyle \lim_{x \rightarrow +\infty} \sqrt{x-2}-\sqrt{x}$
On pourra utiliser l'expression conjuguée de $\sqrt{x-2}-\sqrt{x}$Cas d'indétermination
$+\infty-\infty$
$0\times \pm \infty$
$\dfrac{\pm \infty}{\pm \infty}$
$\dfrac{0}{0}$
Attention, les écritures ci-dessus remplacent les limites mais sont incorrectes...Pour lever l'indétermination, on peut multiplier par l'expression conjuguée de $\sqrt{x-2}-\sqrt{x}$ au numérateur et au dénominateurPour tout réel $x>2$, on a:
Il y a indétermination car $\displaystyle \lim_{x \rightarrow +\infty} \sqrt{x-2}=+\infty$ et $\displaystyle \lim_{x \rightarrow +\infty} -x=-\infty$ donc la limite de la somme est indéterminée.
$\sqrt{x-2}-\sqrt{x}=\dfrac{(\sqrt{x-2}-\sqrt{x})\times (\sqrt{x-2}+\sqrt{x})}{\sqrt{x-2}+\sqrt{x}}$
$\phantom{\sqrt{x-2}-\sqrt{x}}=\dfrac{\sqrt{x-2}^2-\sqrt{x}^2}{\sqrt{x-2}+\sqrt{x}}$
$\phantom{\sqrt{x-2}-\sqrt{x}}=\dfrac{x-2-x}{\sqrt{x-2}+\sqrt{x}}$
$\phantom{\sqrt{x-2}-\sqrt{x}}=\dfrac{-2}{\sqrt{x-2}+\sqrt{x}}$
$\displaystyle \lim_{x \rightarrow +\infty} \sqrt{x-2}=+\infty$ et $\displaystyle \lim_{x \rightarrow +\infty} x=+\infty$
donc par somme $\displaystyle \lim_{x \rightarrow +\infty} \sqrt{x-2}+\sqrt{x}=+\infty$
Exercice 3 (6 points)La fonction $f$ est définie par $f(x)=\dfrac{x^2-2}{x^2+4x-5}$ sur $D_f$ et on note $C_f$ sa représentation graphique de $f$.- Déterminer $D_f$
- Dresser le tableau de signes de $x^2+4x-5$.
$x^2+4x-5$ est du signe de $a=1$ coefficient de $x^2$ donc on a:
- En déduire les limites de $f$ en $x=-5$ et en $x=1$.
Il faut chercher la limite du numérateur et du dénominateur pour $x\longrightarrow -5^-$, $x\longrightarrow -5^+$, $x\longrightarrow 1^-$ puis $x\longrightarrow 1^+$
On pourra utiliser la question précédente pour déterminer le signe du dénominateur.Limite quand $x\longrightarrow -5$
$\displaystyle \lim_{x \rightarrow -5}x^2-2=(-5)^2-2=23$
Limite quand $x \longrightarrow -5^-$ ($x <-5$)
$\displaystyle \lim_{x \rightarrow -5^-}x^2+4x-5=0^+$ puisque $x^2+4x-5 >0$ pour $x <-5$ (voir tableau de signes de $x^2+4x-5$)
Limite quand $x \longrightarrow -5^+$ ($x >-5$)
$\displaystyle \lim_{x \rightarrow -5^+}x^2+4x-5=0^-$ puisque $x^2+4x-5 <0$ pour $x >-5$ (voir tableau de signes de $x^2+4x-5$)
Limite quand $x\longrightarrow 1$
$\displaystyle \lim_{x \rightarrow 1}x^2-2=1^2-2=-1$
Limite quand $x \longrightarrow 1^-$ ($x <1$)
$\displaystyle \lim_{x \rightarrow 1^-}x^2+4x-5=0^-$ puisque $x^2+4x-5 <0$ pour $x <1$ (voir tableau de signes de $x^2+4x-5$)
Limite quand $x \longrightarrow 1^+$ ($x >1$)
$\displaystyle \lim_{x \rightarrow 1^+}x^2+4x-5=0^+$ puisque $x^2+4x-5 >0$ pour $x >1$ (voir tableau de signes de $x^2+4x-5$)
On peut en déduire que les droites d'équations $x=-5$ et $x=1$ sont asymptotes à la courbe $C_f$. - On admet que $\displaystyle \lim_{x \rightarrow -\infty}f(x)= \displaystyle \lim_{x \rightarrow +\infty }f(x)=1$.
Que peut-on en déduire pour la courbe $C_f$?
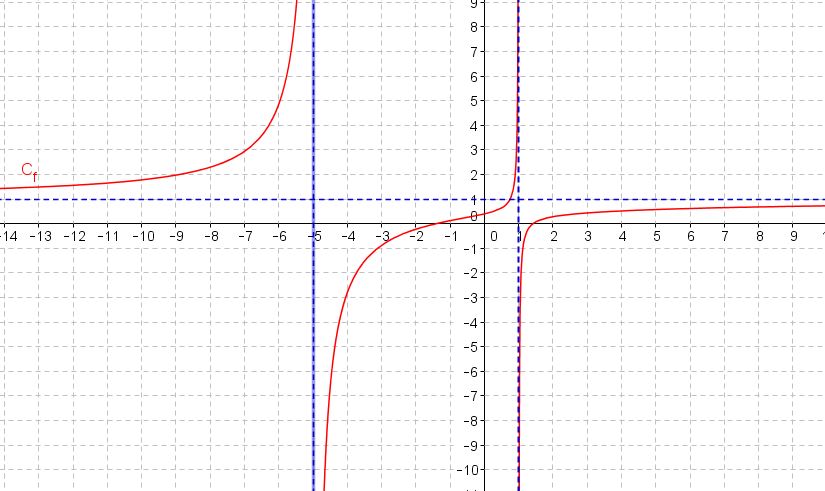
Compléter le tracé de $C_f$ ci-dessous ainsi que les asymptotes à la courbe $C_f$.limite $l$ en $+\infty$ et interprétation graphique
La fonction $f$ est définie sur un intervalle $[a;+\infty[$ et $\ell \in \mathbb{R}$.
$\displaystyle \lim_{x \rightarrow +\infty}f(x)=\ell$ si pour tout intervalle ouvert I contenant $\ell$, il existe $x_0$ tel que pour tout $x>x_0$ on a $f(x)\in $ I
La droite d'équation $y=\ell$ est asymptote à la courbe en $+\infty$On peut déterminer alors l'asymptote à la courbe $C_f$ en $-\infty$ et $+\infty$
Il faut tracer les droites d'équations $x=-5$, $x=1$ et $y=1$.
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.réf 1116: Limites usuelles et opérations
| 5-7mn |
réf 1117: Limites usuelles et opérations
| 5-7mn |
- $\displaystyle \lim_{x \rightarrow +\infty} \sqrt{x-2}-\sqrt{x}$