$\phantom{\Longleftrightarrow} x^2+y^2-2kx-4ky+4k-1=0$

$\Longleftrightarrow (x-k)^2-k^2+(y-2k)^2-4k^2+4k-1=0$

$\Longleftrightarrow (x-k)^2+(y-2k)^2=5k^2-4k+1$
$\mathcal{C}_k$ existe si $5k^2-4k+1\geq 0$

Etude du signe et recherche des racines de $5k^2-4k+1$
$\Delta=b^2-4ac=(-4)^2-4\times 5\times 1=16-20=-4$
$\Delta<0$ donc le polynôme $5k^2-4k+1$ est de signe constant et du signe de $a=5$ coefficient de $x^2$
donc $5k^2-4k+1>0$ pour tout réel $k$.
$\mathcal{C}_k$ a alors pour centre $\Omega_k(k;2k)$ et pour rayon $r_k=\sqrt{5k^2-4k+1}$
$\mathcal{C}_k$ a pour centre $\Omega_k(k;2k)$ et pour rayon $r_k=\sqrt{5k^2-4k+1}$

Pour $k=0$:
$\mathcal{C}_0$ a pour équation $x^2+y^2=1$, pour centre $\Omega_0(0;0)$ et rayon $r_0=1$

Pour $k=1$:
$\mathcal{C}_1$ a pour équation $(x-1)^2+(y-2)^2=5-4+1=2$, pour centre $\Omega_1(1;2)$ et rayon $r_0=\sqrt{2}$

Pour $k=2$:
$\mathcal{C}_2$ a pour équation $(x-2)^2+(y-4)^2=5\times 4-4\times 2+1=13$, pour centre $\Omega_2(2;4)$ et rayon $r_2=\sqrt{13}$

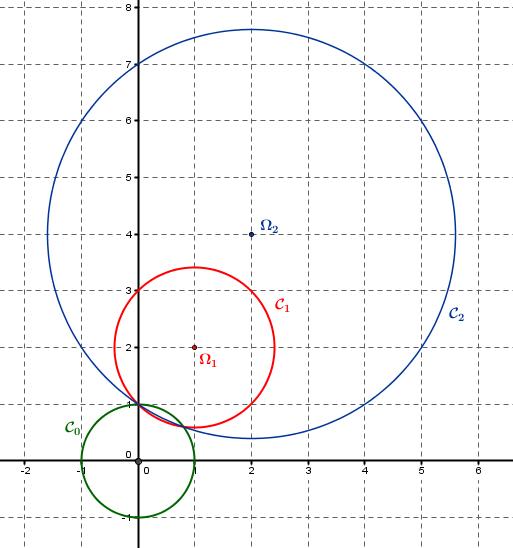
Il semble que les cercles passent par deux points fixes.

équation de $\mathcal{C}_1$:
$(x-1)^2+(y-2)^2=2 \Longleftrightarrow x^2-2x+1+y^2-4y+4-2=0 \Longleftrightarrow x^2-2x+y^2-4y+3=0$
Il faut résoudre le système formé avec les équations de $\mathcal{C}_0$ et $\mathcal{C}_1$:
$\phantom{\Longleftrightarrow}\begin{cases} x^2+y^2=1 \\ x^2-2x+y^2-4y+3=0 \end{cases}$

$\Longleftrightarrow \begin{cases} x^2+y^2-1=0 \\ x^2-2x+y^2-4y+3=x^2+y^2-1 \end{cases}$

$\Longleftrightarrow \begin{cases} x^2+y^2-1=0 \\ -2x-4y+3=-1 \end{cases}$

$\Longleftrightarrow \begin{cases} x^2+y^2-1=0 \\ -2x-4y+4=0 \end{cases}$

$\Longleftrightarrow \begin{cases} x^2+y^2-1=0 \\ -2x-4y+4=0 \end{cases}$

$\Longleftrightarrow \begin{cases} x^2+y^2-1=0 \\ -x-2y+2=0 ~~\text{on divise les deux membres par 2} \end{cases}$

$\Longleftrightarrow \begin{cases} (-2y+2)^2+y^2-1=0 ~~\text{On remplce }x^2 \text{ par }-2y+2 \\ -2y+2=x \end{cases}$

$\Longleftrightarrow \begin{cases} 4y^2-8y+4+y^2-1=0 \\ -2y+2=x \end{cases}$

$\Longleftrightarrow \begin{cases} 5y^2-8y+3=0 \\ -2y+2=x \end{cases}$
Recherche des racines de $5y^2-8y+3$:
$5-8+3=0$ donc $y_1=1$ est une racine de $5y^2-8y+3$
$y_1y_2=\dfrac{c}{a}=\dfrac{3}{5}$ donc $y_2=\dfrac{3}{5}$
$y=-2x+2$ donc $x_1=-2y_1+2=-2+2=0$
et $x_2=-2y_2+2=-2\times \dfrac{3}{5}+2=0\dfrac{4}{5}$
Les points d'intersection de $\mathcal{C}_0$ et $\mathcal{C}_2$ sont $A(0;1)$ et $B(\dfrac{4}{5};\dfrac{3}{5})$

$A(0;1)$:
$x_A^2+y_A^2-2kx_A-4ky_A+4k-1=0+1-0-4k+4k-1=0$
donc $A\in \mathcal{C}_k$ quelque soit la valeur de $k$.
$B(\dfrac{4}{5};\dfrac{3}{5})$:
$x_B^2+y_B^2-2kx_B-4ky_B+4k-1=\dfrac{16}{25}+\dfrac{9}{25}-\dfrac{8k}{5}-\dfrac{12k}{5}+4k-1$
$\phantom{x_B^2+y_B^2-2kx_B-4ky_B+4k-1}=1-\dfrac{20k}{5}+4k-1$
$\phantom{x_B^2+y_B^2-2kx_B-4ky_B+4k-1}=-4k+4k$
$\phantom{x_B^2+y_B^2-2kx_B-4ky_B+4k-1}=0$
donc $B\in \mathcal{C}_k$ quelque soit la valeur de $k$.
Pour tout réel $k$, $\mathcal{C}_k$ passe par les points $A$ et $B$