Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
On note $\mathcal{C}$ le cercle de centre $O$ et de rayon $r$ et $M$ est un point n'appartenant pas à $\mathcal{C}$.
$(d)$ est une droite par $M$ et coupant $\mathcal{C}$ respectivement en deux points distincts $A$ et $B$.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
$(d)$ est une droite par $M$ et coupant $\mathcal{C}$ respectivement en deux points distincts $A$ et $B$.
- Faire une figure avec GEOGEBRA en prenant pour rayon $r$ 5 unités et en plaçant $M$ à l'extérieur du cercle et un point $A$ sur $\mathcal{C}$.
Que peut-on alors conjecturer pour le produit scalaire $ \overrightarrow{MA}. \overrightarrow{MB}$ lorsque $A$ décrit le cercle $\mathcal{C}$?
Refaire la figure avec $M$ à l'intérieur du cercle.
Quelle conjecture peut-on faire sur le signe de $ \overrightarrow{MA}. \overrightarrow{MB}$ selon la position de $M$?Utiliser la commande ProduitScalaire[u,v] pour afficher le produit scalaire $ \overrightarrow{u}. \overrightarrow{v}$ en définissant $ \overrightarrow{u}= \overrightarrow{MA}$ et $ \overrightarrow{v}= \overrightarrow{MB}$Placer le point $O$
Tracer le cercle de centre $O$ et rayon 5 (commande "cercle-centre-rayon")
Placer le point $M$ à l'extérieur de $\mathcal{C}$.
Tracer une droite $(d)$ passant par $M$ et un point du cercle.
Marquer $B$ intersection du cercle et de la droite $(d)$
Tracer les vecteurs $ \overrightarrow{u}= \overrightarrow{MA}$ et $ \overrightarrow{v}= \overrightarrow{MB}$ puis afficher le produit scalaire $ \overrightarrow{MA}. \overrightarrow{MB}$ (commande: \rg{ProduitScalaire[u,v]} dans la barre de saisie)
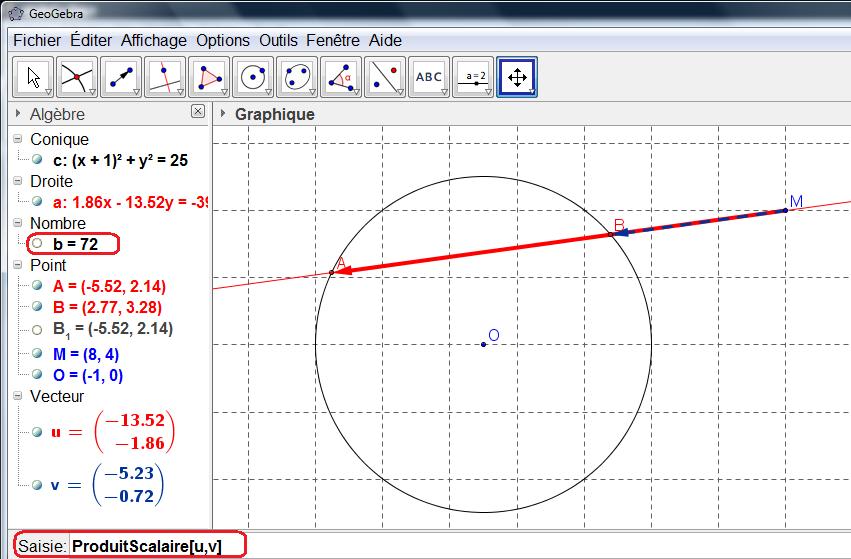
Ouvrir le fichier GEOGEBRA de la figure
En plaçant $M$ à l'intérieur du cercle, on a:
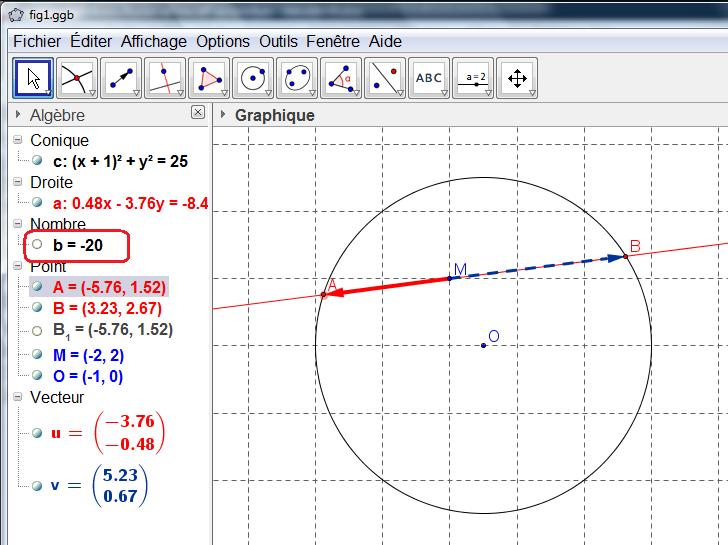
- On note $A'$ le point du cercle diamétralement opposé au point $A$.
Montrer que $ \overrightarrow{MA}. \overrightarrow{MB}= \overrightarrow{MA}. \overrightarrow{MA`}$Propriétés du produit scalaire
Soient $\overrightarrow{u}$, $\overrightarrow{v}$ et $\overrightarrow{w}$ trois vecteurs et $k$ un réel:
$\overrightarrow{u}.\overrightarrow{v}=\overrightarrow{v}.\overrightarrow{u}$
$(k \overrightarrow{u}).\overrightarrow{v}=k(\overrightarrow{u}.\overrightarrow{v})$
$(\overrightarrow{u}+\overrightarrow{v}).\overrightarrow{w}=\overrightarrow{u}.\overrightarrow{w}+\overrightarrow{v}.\overrightarrow{w}$Orthogonalité
Pour tous vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ non nuls, on a:
$\overrightarrow{u}.\overrightarrow{v}=0 \Longleftrightarrow \overrightarrow{u}$ et $\overrightarrow{v}$ sont orthogonaux.Décomposer $ \overrightarrow{MB}= \overrightarrow{MA'}+ \overrightarrow{A'B}$$ \overrightarrow{MA}. \overrightarrow{MB}= \overrightarrow{MA}.( \overrightarrow{MA'}+ \overrightarrow{A'B})$
$\phantom{ \overrightarrow{MA}. \overrightarrow{MB}}= \overrightarrow{MA}. \overrightarrow{MA'}+ \overrightarrow{MA}. \overrightarrow{A'B}$
$[AA']$ est un diamètre du cercle $\mathcal{C}$ et $B\in \mathcal{C}$ donc $ABA'$ est un triangle rectangle en $B$
donc $ \overrightarrow{AB}$ et $ \overrightarrow{A'B}$ sont orthogonaux.
De plus, $B\in (MA)$ donc $ \overrightarrow{MB}$ et $ \overrightarrow{AB}$ sont colinéaires
donc $ \overrightarrow{MB}$ et $ \overrightarrow{A'B}$ sont orthogonaux
donc $ \overrightarrow{MB}. \overrightarrow{A'B}=0$
- En déduire que $ \overrightarrow{MA}. \overrightarrow{MB}=MO^2-r^2$
Utiliser $ \overrightarrow{MA}. \overrightarrow{MA'}$ et décomposer les vecteurs $ \overrightarrow{MA}$ et $ \overrightarrow{MA'}$ en faisant intervenir le centre O du cercle.$ \overrightarrow{MA}. \overrightarrow{MA'}=( \overrightarrow{MO}+ \overrightarrow{OA}).( \overrightarrow{MO}+ \overrightarrow{OA'})$
$\phantom{ \overrightarrow{MA}. \overrightarrow{MA'}}= \overrightarrow{MO}. \overrightarrow{MO}+ \overrightarrow{MO}. \overrightarrow{OA'}+ \overrightarrow{OA}. \overrightarrow{MO}+ \overrightarrow{OA}. \overrightarrow{OA'}$
$\phantom{ \overrightarrow{MA}. \overrightarrow{MA'}}= \overrightarrow{MO}^2+ \overrightarrow{MO}. \overrightarrow{OA'}+ \overrightarrow{MO}. \overrightarrow{OA}+ \overrightarrow{OA}. \overrightarrow{OA'}$
$\phantom{ \overrightarrow{MA}. \overrightarrow{MA'}}=MO^2+ \overrightarrow{MO}.( \overrightarrow{OA'}+ \overrightarrow{OA})+ \overrightarrow{OA}. \overrightarrow{OA'}$
$O$ est le milieu de $[AA']$ donc $ \overrightarrow{AO}= \overrightarrow{OA'}=\dfrac{1}{2} \overrightarrow{AA'}$ et $ \overrightarrow{OA'}+ \overrightarrow{OA}= \overrightarrow{0}$
donc on a:
$ \overrightarrow{MA}. \overrightarrow{MA'}=MO^2+ \overrightarrow{MO}. \overrightarrow{0}+(\dfrac{-1}{2} \overrightarrow{AA'}).(\dfrac{1}{2} \overrightarrow{AA'})$
$\phantom{ \overrightarrow{MA}. \overrightarrow{MA'}}=MO^2-\dfrac{1}{4} \overrightarrow{AA'}^2$
$\phantom{ \overrightarrow{MA}. \overrightarrow{MA'}}=MO^2-\dfrac{1}{4}AA'^2$
$\phantom{ \overrightarrow{MA}. \overrightarrow{MA'}}=MO^2-\dfrac{(2r)^2}{4}$ car $AA'=2OA=2r$
$\phantom{ \overrightarrow{MA}. \overrightarrow{MA'}}=MO^2-r^2$
On retrouve la conjecture faite sur le signe de $ \overrightarrow{MA}. \overrightarrow{MB}$ car si $M$ est à l'intérieur du cercle alors $MO$
et alors $ \overrightarrow{MA}. \overrightarrow{MB}<0$
On a montré que le produit scalaire $ \overrightarrow{MA}. \overrightarrow{MB}$ est indépendant de la position de la droite $(d)$ sécante au cercle $\mathcal{C}$.
Ce produit scalaire ne dépend que de la position de $M$ par rapport à $O$.
Le réel $MO^2-r^2$ est appelé puissance du point $M$ par rapport au cercle $\mathcal{C}$.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
