Publications MATHS-LYCEE.FR
Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
On donne le tableau de variation de la fonction polynôme du second degré $f$ définie sur $\mathbb{R}$.
Déterminer l'expression de chacune de ces fonctions.
Déterminer l'expression de chacune de ces fonctions.
- Tableau 1:
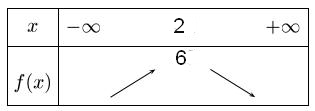
La courbe représentative de $f$ coupe l'axe des ordonnées au point $A$ de coordonnées $(0;3)$.Variations fonction polynôme du second degré
Soit la fonction $P$ définie sur $\mathbb{R}$ par sa forme canonique $P (x) = a(x-\alpha)^2 + \beta$
La courbe représentative de $P$ est une parabole dont le sommet a pour coordonnées $(\alpha; \beta)$.
Tableau de variation: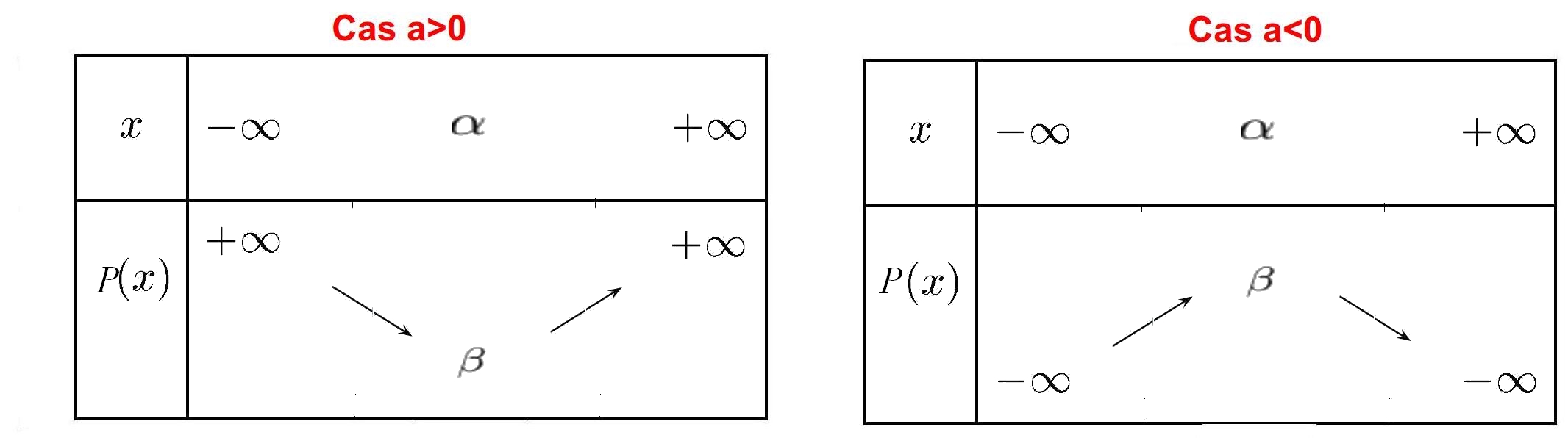
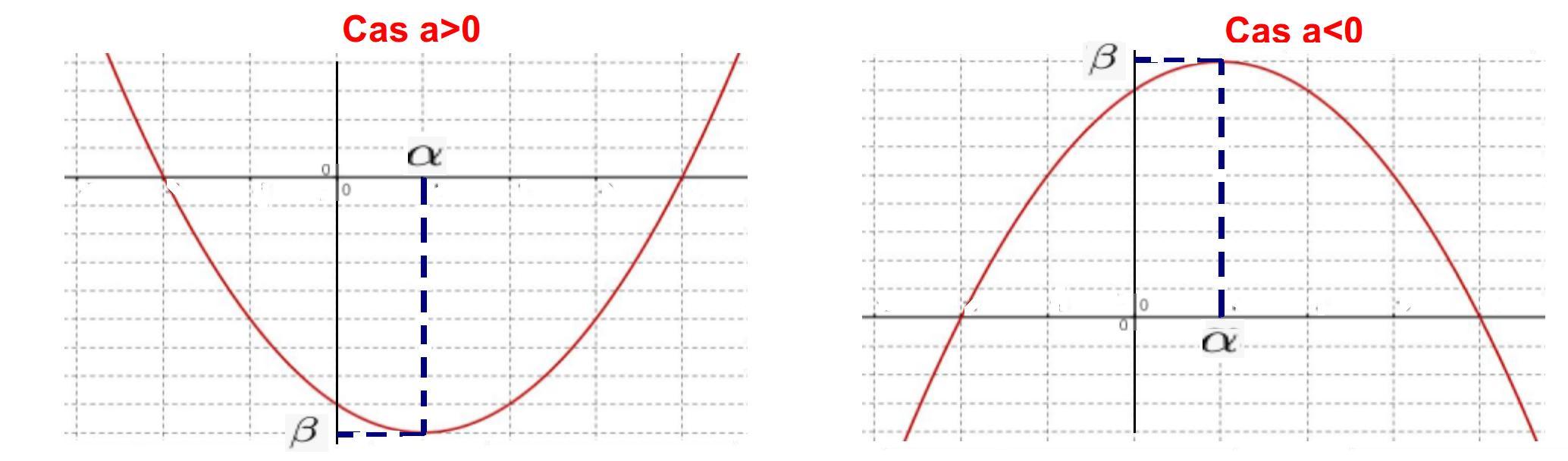Déterminer les coordonnées du sommet de la parabole à laide du tableau de variation pour déterminer $\alpha$ et $\beta$ dans la forme canonique $f(x)=a(x-\alpha)^2+\beta$
On peut déterminer ensuite la valeur de $a$ en utilisant les coordonnées du point $A$ soit $f(0)=3$La forme canonique de $f$ est $f(x)=a(x-\alpha)^2+\beta$.
D'après le tableau de variation, le sommet de la parabole a pour coordonnées $(2;6)$
donc $\alpha=2$ et $\beta=6$
donc $f(x)=a(x-2)^2+6$
Le point $A$ appartient à la courbe représentative de $f$ donc $f(0)=3$.
$f(0)=3 \Longleftrightarrow a(0-2)^2+6=3$
$\phantom{f(0)=3} \Longleftrightarrow a\times (-2)^2=3-6$
$\phantom{f(0)=3} \Longleftrightarrow 4a=-3$
$\phantom{f(0)=3} \Longleftrightarrow a=-\dfrac{3}{4}$
$f$ étant croissante puis décroissante, le coefficient $a$ de $x^2$ est négatif.- Tableau 2:
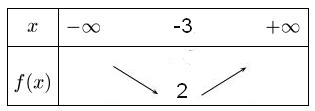
Le point $A$ de coordonnées $(4;16)$ appartient à la courbe représentative de $f$.Déterminer les coordonnées du sommet de la parabole à laide du tableau de variation pour déterminer $\alpha$ et $\beta$ dans la forme canonique $f(x)=a(x-\alpha)^2+\beta$
On peut déterminer ensuite la valeur de $a$ en utilisant les coordonnées du point $A(4;16)$ soit $f(4)=16$La forme canonique de $f$ est $f(x)=a(x-\alpha)^2+\beta$.
D'après le tableau de variation, le sommet de la parabole a pour coordonnées $(-3;2)$
donc $\alpha=-3$ et $\beta=2$
donc $f(x)=a(x-(-3))^2+2=a(x+3)^2+2$ aux deux signes $-$ successifs dans $-\alpha=-(-3)$
Le point $A(4;16)$ appartient à la courbe représentative de $f$ donc $f(4)=16$.
$f(4)=16 \Longleftrightarrow a(4+3)^2+2=16$
$\phantom{f(4)=16} \Longleftrightarrow a\times 7^2=16-2$
$\phantom{f(-2)=0} \Longleftrightarrow 49a=14$
$\phantom{f(-2)=0} \Longleftrightarrow a=\dfrac{14}{49}$
$\phantom{f(-2)=0} \Longleftrightarrow a=\dfrac{2}{7}$ (on peut simplifier la fraction par 7)
- Tableau 3:
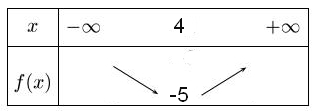
La courbe représentative de $f$ coupe l'axe des abscisses au point $A$ d'abscisse $2$.La forme canonique de $f$ est $f(x)=a(x-\alpha)^2+\beta$.
D'après le tableau de variation, le sommet de la parabole a pour coordonnées $(4;-5)$
donc $\alpha=4$ et $\beta=-5$
donc $f(x)=a(x-4)^2-5$
La courbe représentative de $f$ coupe l'axe des abscisses au point $A$ d'abscisse $2$
donc le point $A(2;0)$ appartient à la courbe représentative de $f$ donc $f(2)=0$.
$f(2)=0 \Longleftrightarrow a(2-4)^2-5=0$
$\phantom{f(2)=0} \Longleftrightarrow a\times (-2)^2=5$
$\phantom{f(2)=0} \Longleftrightarrow 4a=5$
$\phantom{f(2)=0} \Longleftrightarrow a=\dfrac{5}{4}$
$2$ est donc une racine de $f$ puisque $f(2)=0$
$f(2)=\dfrac{5}{4}(2-4)^2-5=\dfrac{5}{4}\times 4-5=5-5=0$
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)vidéos semblables
Pour compléter cet exercice, nous vous conseillons les vidéos suivantes semblables à l'exercice affiché.exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.nº598 Forme canonique et variations
| 6-10mn |
nº602 Forme canonique-variations-forme factorisée
| 5-10mn |
- Tableau 2: