$|z^3|=|z|^3$
donc $|z|^3=1$
donc $|z|=1$

$|z|=1$ donc $z=e^{i\Theta}$ avec $\theta=arg(z)$ $(2\pi)$
Il faut donc résoudre$z^3=\left(e^{i\Theta}\right)^3=e^{i3\Theta}=1=e^{i\times 0}$
$e^{i3\Theta}=e^{i\times 0}$
$\Longleftrightarrow 3\Theta=0+k2\pi$ avec $k\in \mathbb{Z}$
$\Longleftrightarrow \Theta=0+\dfrac{k2\pi}{3}$ avec $k\in \mathbb{Z}$
donc $arg(z)=0+\dfrac{k2\pi}{3}$ avec $k\in \mathbb{Z}$ ou encore $arg(z)=0$ $\left(\dfrac{2\pi}{3}\right)$

Si $k=0$
$z_0=e^{0i}=1$
Si $k=1$
$z_1=e^{i\dfrac{2\pi}{3}}=cos\left(\dfrac{2\pi}{3}\right)+isin\left(\dfrac{2\pi}{3}\right)=\dfrac{-1}{2}+i\dfrac{\sqrt{3}}{2}$
Si $k=2$
$z_2=e^{i\dfrac{4\pi}{3}}=cos\left(\dfrac{4\pi}{3}\right)+isin\left(\dfrac{4\pi}{3}\right)=\dfrac{-1}{2}-i\dfrac{\sqrt{3}}{2}$
Les 3 solutions de cette équation sont $z_0=1$, $z_1=\dfrac{-1}{2}+i\dfrac{\sqrt{3}}{2}$ et $z_2=\dfrac{-1}{2}-i\dfrac{\sqrt{3}}{2}$
Remarque
Si $k=4$ alors $arg(z_3)=\dfrac{6\pi}{3}=0$ $~~(2\pi)$ et donc $z_3=z_0$...

$\dfrac{z_1}{z_0}=\dfrac{e^{i\dfrac{2\pi}{3}}}{e^{0i}}=e^{i\dfrac{2\pi}{3}}$
donc $arg\left( \dfrac{z_1}{z_0} \right)=(\overrightarrow{OM_0};(\overrightarrow{OM_1})=\dfrac{2\pi}{3}$ $(2\pi)$
$\dfrac{z_2}{z_1}=\dfrac{e^{i\dfrac{4\pi}{3}}}{e^{i\dfrac{4\pi}{3}}}=e^{i\dfrac{2\pi}{3}}$
$arg\left( \dfrac{z_2}{z_1} \right)=(\overrightarrow{OM_1};(\overrightarrow{OM_2})=\dfrac{2\pi}{3}$ $(2\pi)$
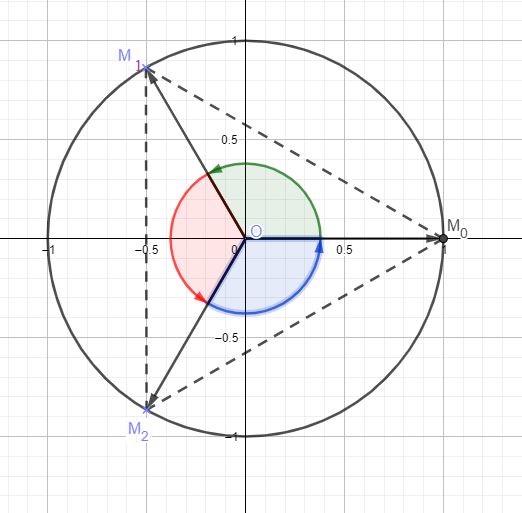
donc $M_0$, $M_1$ et $M_2$ sont les sommets d'un polygône régulier à 3 côtés (voir figure)
$M_0M_1M_2$ est un triangle équilatéral.