Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
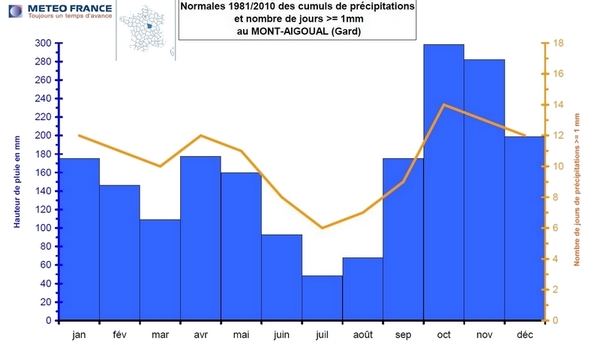
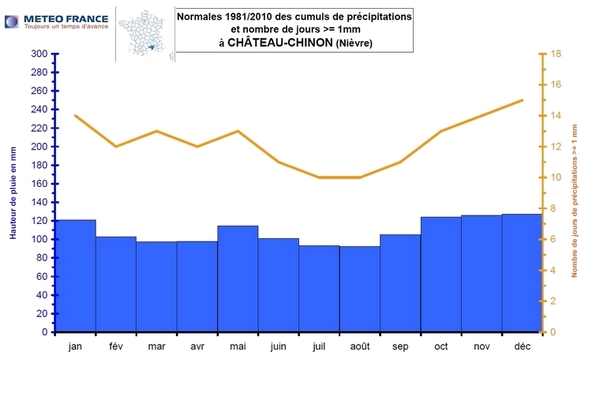
Les graphiques ci-dessous permettent de comparer les différents régimes pluviométriques de 2 stations avec une pluviométrie annuelle forte (supérieure à 1200 mm voire 2000 mm par an): Château-Chinon (Nièvre) et mont-Aigoual (Gard).
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)


- Calculer la hauteur de pluie moyenne et l'écart correspondant pour chacune de ces deux villes pour la période des relevés.
Interpréter et commenter les résultats.Moyenne
On considère la série de $N$ données $x_i$ ($i$ entier naturel compris entre $1$ et $N$) les valeurs du caractère et $n_i$ les effectifs correspondants.
$N=n_1+n_2+$.... est l'effectif total.
La moyenne de la série statistique est $\overline{x}=\dfrac{n_1x_1+n_2x_2+\text{.....}+n_px_p}{N}$.} Dans le cas d'une série regroupée en classe, on utilise le centre des classes pour faire le calcul de la moyenne.Écart type et variance
La variance (notée le plus souvent $V$) est la moyenne des carrés des écarts à la moyenne.
$V=\dfrac{n_1(\overline{x}-x_1)^2+n_2(\overline{x}-x_2)^2..............+n_p(\overline{x}-x_p)^2}{N}$
On peut aussi calculer $V$ plus simplement:
$V=\dfrac{(n_1x_1^2+n_2x_2^2+........n_p x_p^2)}{N}-\overline{x}^2$
L'écart type noté $\sigma $ est $\sigma=\sqrt{V}$
L'écart type est une caractéristique de dispersion.Lire sur le graphique les hauteurs correspondantes pour chaque mois de l'année
Il n'y a pas d'effectifs donc il faut paramétrer la calculatrice avec 1VAR XLIST: list1 et 1VAR Freq: 1.Pour la ville de Mont-Aigoual, on a:
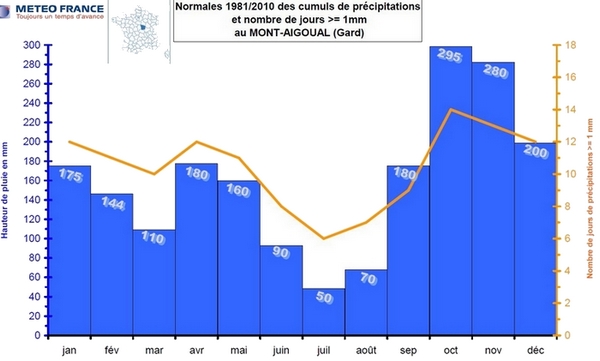
$\overline{h_1}=\dfrac{175+144+110+180+160+90+50+70+180+295+280}{12}\approx 161$
$V_1=\dfrac{175^2+144^2+110^2+180^2+160^2+90^2+50^2+70^2+180^2+295^2+280^2}{12}-\overline{h_1}$
et $\sigma_1=\sqrt{V_1} \approx 72,5$
Pour la ville de Château-Chinon, on a:
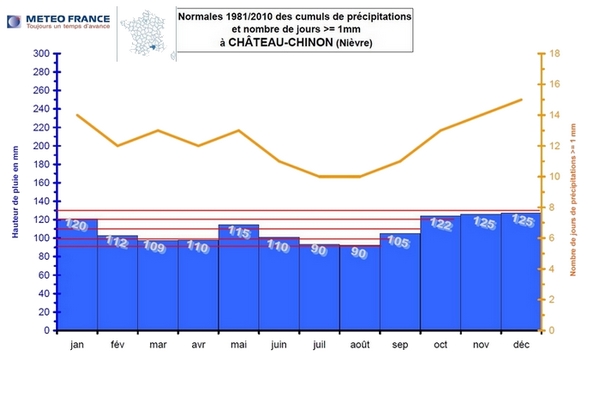
$\overline{h_2}=\dfrac{120+112+109+110+115+110+90+90+105+122+124+125}{12}\approx 111$
et $\sigma_2 \approx 11,2$
La hauteur moyenne mensuelle est supérieure dans le sud et les différences entre les plus grandes hauteurs et les plus faibles est beaucoup plus grande, les valeurs sont très dispersées par rapport à la moyenne.
Ce que l'on constate également facilement sur les deux graphiques. - Calculer la le nombre de jours moyen mensuel où la hauteur des précipitations est supérieure à 1mm et l'écart correspondant pour chacune de ces deux villes pour la période des relevés.
Interpréter et commenter les résultats.
Les relevés sont les suivants (nombre de jours):

Pour la ville de Mont-Aigoual, on a:
$\overline{n_1}=\dfrac{12+11+10+12+11+8+6+7+9+14+13+12}{12}\approx 10,4$
Pour la ville de Château-Chinon, on a:
$\overline{n_2}=\dfrac{14+12+13+12+13+11+10+10+11+13+14+15}{12}\approx 12,3$
La hauteur moyenne mensuelle est supérieure dans le sud mais le nombre de jours de pluie par mois est supérieur à Château-Chinon.
Il pleut donc plus longtemps à Château-Chinon mais avec des précipitations moins fortes, ce qui explique différence entre nombre de jours de pluie et hauteur des précipitations entre les deux villes.
Compléments: La station de Château-Chinon est très représentative du climat océanique altéré, avec un important effet orographique.
Située sur le versant nord-ouest du Morvan, à 600 mètres d'altitude, les pluies sont soutenues tout au long de l'année, malgré un léger répit en juillet et en août. Les perturbations atlantiques, et celles qui descendent du nord de l'Europe se réactivent sensiblement sur ces premiers reliefs conséquents qu'elles rencontrent sur leur trajet.
Cette région du Morvan, qui alimente le bassin de l'Yonne, joue un rôle important dans les niveaux des crues de la Seine à Paris.
Au mont Aigoual, à 1567 m d'altitude sur l'arc cévenol, les précipitations ont un régime méditerranéen (sécheresse estivale et fortes pluies automnales) avec des quantités beaucoup plus importantes (plus de 2 mètres d'eau par an et des records en 24 heures dépassant 500 mm comme le 30 octobre 1963 ou le 25 février 1964).
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
