Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
On a effectué une étude sur la durée des communications au standard téléphonique d'une grande entreprise.
Les durées données en seconde sont regroupées en classes de même amplitude.

Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Les durées données en seconde sont regroupées en classes de même amplitude.

- Compléter le tableau
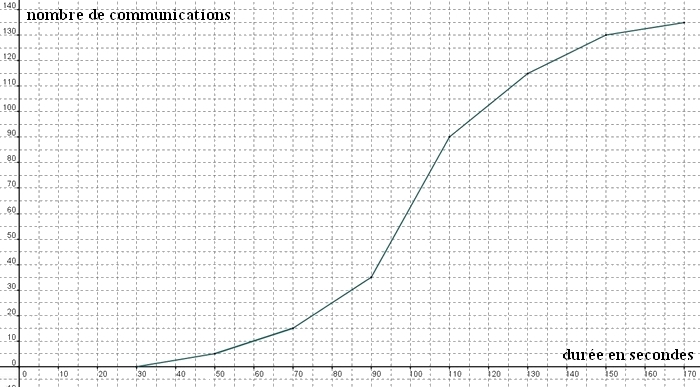
- Construire le diagramme des effectifs cumulés croissants en prenant 1cm pour 10 secondes et 1 cm pour 10 communications.
Attention, l'effectif cumulé 15 signifie que 15 communications durent moins de 70 secondes, il faut donc placer le point de coordonnées (70;15).
L'effectif cumulé 20 signifie que 35 communications durent moins de 90 secondesL'effectif cumulé 15 signifie que 15 communications durent moins de 70 secondes, il faut donc placer le point de coordonnées (70;15)
de même, il faut placer le points (90;35) (35 communications de moins de 90 secondes), le point (110;90)....
- Déterminer graphiquement la valeur de $Q_1$ (premier quartile), de la médiane et de $Q_3$ (troisième quartile)
Quartiles
Le premier quartile $Q_1$ est la plus petite valeur du caractère telle que au moins 25% (un quart) des valeurs soient inférieures ou égales à $Q_1$.
Le troisième quartile $Q_3$ est la plus petite valeur du caractère telle que au moins 75% (trois quarts) des valeurs soient inférieures ou égales à $Q_3$.
L'intervalle $[Q_1;Q_3]$ est l'intervalle interquartile et $Q_3-Q_1$ est l'écart interquartile.Médiane
La médiane $M$ est la valeur du caractère telle que a 50% (la moitié) des valeurs soient inférieures ou égales à $M$ et l'autre moitié supérieures ou égale à $M$.
Exemple 1: Si l'effectif total est pair (par exemple 14 valeurs) alors la médiane est entre la 7ième et la 8ième valeur(valeurs classées dans l'ordre croissant)
Exemple 2: Si l'effectif total est impair (par exemple 15 valeurs) alors la médiane correspond à la 8ième valeur(valeurs classées dans l'ordre croissant)25% de 135 est égal à 33,75.
75% de 135 est égal à 101,25.
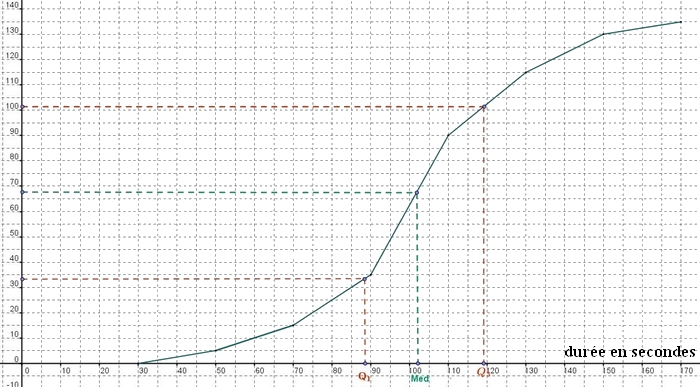
Graphiquement, on a donc:
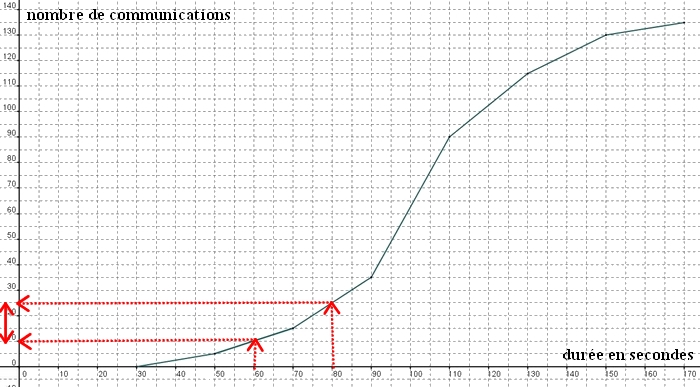
- En utilisant le graphique, déterminer combien de communications ont une durée comprise entre 60 et 80s?
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
vidéos semblables
Pour compléter cet exercice, nous vous conseillons les vidéos suivantes semblables à l'exercice affiché.
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.