Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
Dans le plan muni d'un repère orthonormé, déterminer dans chaque cas si les points A, B et C sont alignés
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
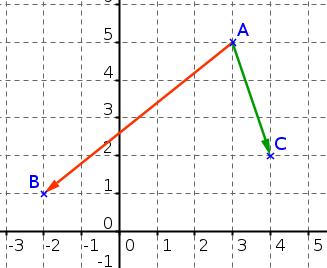
- $A(3;5)$, $B(-2;1)$ et $C(4;2)$
Coordonnées d'un vecteur défini par deux points
Si $A(x_A;y_A)$ et $B(x_B;y_B)$ alors $\overrightarrow{AB}(x_B-x_A;y_B-y_A)$ (coordonnées du second point $-$ coordonnées du premier point)Critère de colinéarité dans un repère
Dans un repère du plan, $\overrightarrow{u}(x;y)$ et $\overrightarrow{w}(x'y')$ non nuls sont colinéaires si et seulement si $xy'-x'y=0$Calculer les coordonnées des vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$ pour déterminer si les deux vecteurs sont colinéaires
Les trois points A, B et C sont alignés si les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$(ou bien $\overrightarrow{BC}$) sont colinéaires$\begin{cases} x_{\overrightarrow{AB}}=x_B-x_A=-2-3=-5 \\ y_{\overrightarrow{AB}}=y_B-y_A=1-5=-4 \end{cases}$
donc $\overrightarrow{AB}(-5;-4)$
$\begin{cases} x_{\overrightarrow{AC}}=x_C-x_A=4-3=1 \\ y_{\overrightarrow{AC}}=y_C-y_A=2-5=-3 \end{cases}$
donc $\overrightarrow{AC}(1;-3)$
$ x_{\overrightarrow{AB}}y_{\overrightarrow{AC}}-y_{\overrightarrow{AB}}x_{\overrightarrow{AC}}=(-5)\times (-3)-(-4)\times 1=19$
donc les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$ ne sont pas colinéaires
Penser à placer les points dans un repère pour contrôler le résultat obtenu par le calcul.
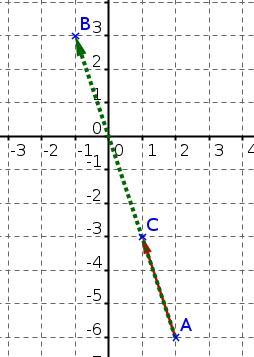
- $A(2;-6)$, $B(-1;3)$ et $C(1;-3)$
$\begin{cases} x_{\overrightarrow{AB}}=x_B-x_A=-1-2=-3 \\ y_{\overrightarrow{AB}}=y_B-y_A=3-(-6)=9 \end{cases}$
donc $\overrightarrow{AB}(-3;9)$
$\begin{cases} x_{\overrightarrow{AC}}=x_C-x_A=1-2=-1 \\ y_{\overrightarrow{AC}}=y_C-y_A=-3-(-6)=3 \end{cases}$
donc $\overrightarrow{AC}(-1;3)$
$x_{\overrightarrow{AB}}y_{\overrightarrow{AC}}-y_{\overrightarrow{AB}}x_{\overrightarrow{AC}}=(-3)\times 3-9\times (-1)=-9+9=0$
donc les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$ sont colinéaires
Penser à placer les points dans un repère pour contrôler le résultat obtenu par le calcul.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Fiche méthode
Si cet exercice vous pose problème, nous vous conseillons de consulter la fiche méthhode.
Vecteurs colinéaires et alignement
- montrer que trois points sont alignés dans un repère
- utiliser le critère de colinéarité
infos: | 10mn |
vidéos semblables
Pour compléter cet exercice, nous vous conseillons les vidéos suivantes semblables à l'exercice affiché.
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
