Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
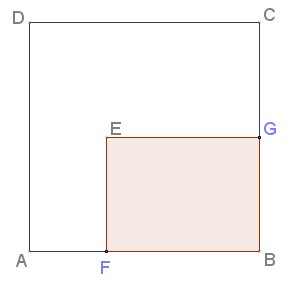
Sur la figure ci-dessous, $ABCD$ est un carré de côté $x$ cm et on a $AF=2cm$ et $CG=3$ cm.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)

- Montrer que pour tout réel $x$ on a $x^2-10x=(x-5)^2-25$.
Identités remarquables
$(a+b)^2=a^2+2ab+b^2$
$(a-b)^2=a^2-2ab+b^2$
$(a-b)(a+b)=a^2-b^2$
On peut développer $(x-5)^2-25$$(x-5)^2-25=x^2-2\times x\times 5+5^2-25=x^2-10x$
-
Peut-on trouver un carré $ABCD$ tel que l'aire du rectangle $BGEF$ soit égale à l'aire du polygone $ADCGEF$?
Il faut exprimer l'aire de chacun des polygone en fonction de $x$On a $AB=x$ et $AF=2$ donc $BF=x-2$.
On a $BC=x$ et $GC=3$ donc $BG=x-3$.
L'aire $A$ du rectangle $BGEF$ est donc $A=(x-2)(x-3)$ cm$^2$.
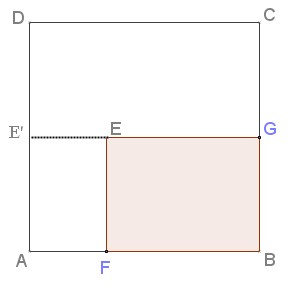
On a $AE'=x-3$ et $AF=2$ donc $A_{AFEE'}=2(x-3)=2x-6$ cm$^2$
et $A_{DCGE'}=3x$
donc l'aire $A'$ du quadrilatère $ADCGEF$ est $A=2x-6+3x=5x-6$.
On peut aussi calculer l'aire du polygone $ADCGEF$ en enlevant l'aire du rectangle $BGEF$ à celle du carré $ABCD$ et on a alors:
$A=x^2-(x-3)(x-2)=x^2-(x^2-3x-2x+6)=5x-6$
Il faut donc résoudre l'équation $(x-2)(x-3)=5x-6$
$(x-2)(x-3)=5x-6\Longleftrightarrow x^2-3x-2x+6=5x-6$
$\phantom{(x-2)(x-3)=5x-6} \Longleftrightarrow x^2-5x+6-5x+6=0$
$\phantom{(x-2)(x-3)=5x-6} \Longleftrightarrow x^2-10x+12=0$
Il faut factoriser $x^2-10x+12$.
$x^2-10x+12=(x-5)^2-25+12$
$\phantom{x^2-10x+12}=(x-5)^2-13$
$\phantom{x^2-10x+12}=(x-5)^2-\sqrt{13}^2$
$\phantom{x^2-10x+12}=(x-5-\sqrt{13})(x-5+\sqrt{13})$
donc on a: $x^2-10x+12=0 \Longleftrightarrow (x-5-\sqrt{13})(x-5+\sqrt{13})=0$
$\phantom{x^2-10x+12=0} \Longleftrightarrow x-5-\sqrt{13}=0$ ou $x-5+\sqrt{13}=0$
$\phantom{x^2-10x+12=0} \Longleftrightarrow x=5+\sqrt{13}$ ou $x=5-\sqrt{13}$
$5+\sqrt{13}\approx 8,6$ et $5-\sqrt{13}\approx 1,4$
Comme $CG=3$ alors la distance $CB$ est supérieure à 3 donc $x\geq 3$
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
