Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
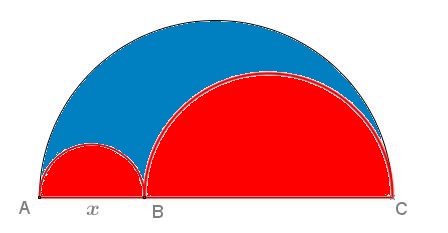
Sur la figure ci-dessous, on a $AC=10cm$ et on pose $AB=x$ avec $x\in ]0;10[$.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)

- Exprimer $BC$ en fonction de $x$.
$B\in [AC]$ donc $BC=AC-AB=10-x$.
- Exprimer l'aire $A$ des deux demi-disques rouges sur la figure en fonction de $x$.
Rappel: l'aire d'un disque de rayon $R$ est $\pi R^2$On note $A_1$ l'aire du demi-disque de diamètre $[AB]$.
Le rayon de ce demi-disque est $R_1=\dfrac{AB}{2}=\dfrac{x}{2}$
$A_1=\dfrac{1}{2}(\pi R_1^2)=\dfrac{1}{2}\times \pi \left(\dfrac{x}{2}\right)^2=\dfrac{1}{2}\times \dfrac{\pi x^2}{4}=\dfrac{\pi x^2}{8}$
On note $A_2$ l'aire du demi-disque de diamètre $[BC]$.
Le rayon de ce demi-disque est $R_2=\dfrac{BC}{2}=\dfrac{10-x}{2}$
$A_2=\dfrac{1}{2}(\pi R_2^2)$
$\phantom{A_2}=\dfrac{1}{2}\times \pi \left(\dfrac{10-x}{2}\right)^2$
$\phantom{A_2}= \dfrac{\pi(10-x)^2}{8}$
L'aire totale des deux demi-disques rouges est donc:
$A=A_1+A_2=\dfrac{\pi x^2}{8}+\dfrac{\pi(10-x)^2}{8}= \dfrac{\pi}{8} ( x^2+(10-x)^2)$
- Peut-on placer $B$ distinct de $A$ et de $C$ sur le segment $[AC]$ pour que l'aire bleue soit égale à l'aire rouge?
Identités remarquables
$(a+b)^2=a^2+2ab+b^2$
$(a-b)^2=a^2-2ab+b^2$
$(a-b)(a+b)=a^2-b^2$
L'aire bleue est $A'=\dfrac{1}{2}\times \pi \times 5^2-A$ (aire du grand demi-disque de diamètre $[AC]-$ aire rouge)
$A'=A \Longleftrightarrow A=\dfrac{1}{2}\times \pi \times 5^2-A$
$\phantom{A'=A} \Longleftrightarrow 2A=\dfrac{25 \pi}{2}$
$\phantom{A'=A} \Longleftrightarrow 2\times \dfrac{\pi}{8} ( x^2+(10-x)^2)=\dfrac{25 \pi}{2}$
$\phantom{A'=A} \Longleftrightarrow \dfrac{\pi}{4} ( x^2+(10-x)^2)=\dfrac{25 \pi}{2}$
$\phantom{A'=A} \Longleftrightarrow x^2+(10-x)^2=\dfrac{25 \pi}{2}\times \dfrac{4}{\pi}$
$\phantom{A'=A} \Longleftrightarrow x^2+100-20x+x^2=50$
$\phantom{A'=A} \Longleftrightarrow 2 x^2+100-20x-50=0$
$\phantom{A'=A} \Longleftrightarrow 2 x^2-20x+50=0$ (on peut diviser les deux membres par 2)
$\phantom{A'=A} \Longleftrightarrow x^2-10x+25=0$
$\phantom{A'=A} \Longleftrightarrow (x-5)^2=0$
$\phantom{A'=A} \Longleftrightarrow x-5=0$
$\phantom{A'=A} \Longleftrightarrow x=5$
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
