1. Home
  2. chapitre 2 Dérivation
  3. exercice corrigé nº765
PDF reservé aux abonnés
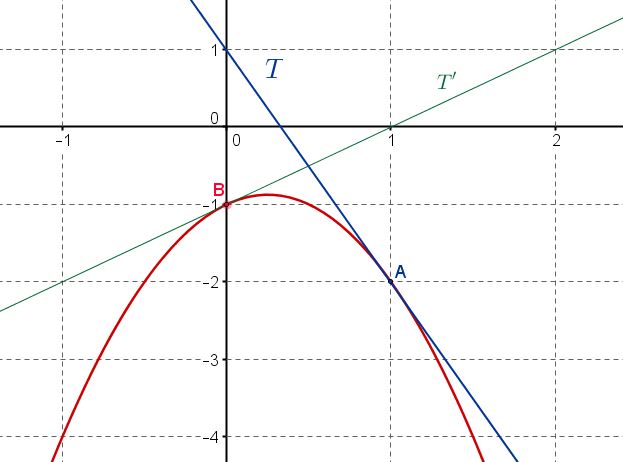
La fonction $f$ est définie et dérivable sur $\mathbb{R}$ par $f(x)=-2x^2+x-1$.
On donne ci-dessous la représentation graphique $C_f$ de la fonction $f$ dans un repère orthogonal.

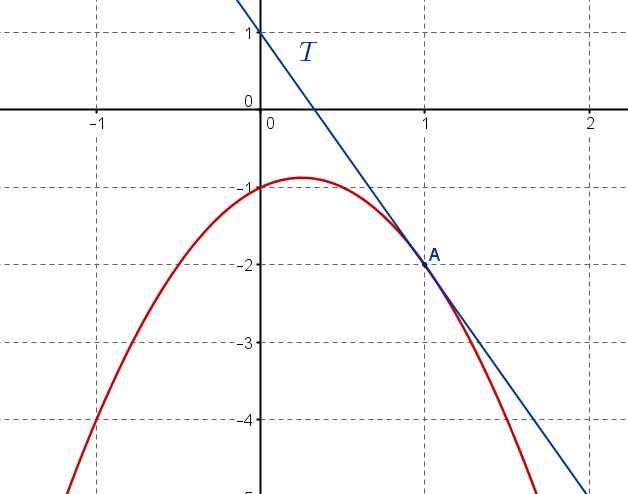
  1. Le nombre dérivé de $f$ en $x=1$ est $f'(1)=-3$.
    Déterminer l'équation réduite de la tangente $T$ à la courbe au point d'abscisse 1 et la tracer dans le repère ci-dessus.

    Rappel de cours

    Équation de la tangente au point d'abscisse $a$

    $f$ est une fonction définie et dérivable en $x=a$.
    La tangente à $C_f$ en $a$ a pour coefficient directeur $f'(a)$
    et pour équation réduite $ y=f'(a)(x-a)+f(a)$}

    Aide

    Il faut calculer $f(1)$

    Solution

    $f(1)=-2\times (1)^2+1-1=-2$
    Avec le résultat du cours $y=f'(a)(x-a)+f(a)$ et ici $a=1$, on a:
    $y=f~'(1)(x-1)+f(1)$
    $\phantom{y}=-3(x-1)-2$
    $\phantom{y}=-3x+3-2$
    $\phantom{y}=-3x+1$

    $T$ passe par le point $A(1;-2)$ et a pour coefficient directeur $-3$.
    $T$ coupe l'axe des ordonnées au point d'ordonnée 1, pour $x=0$ on a $y=1$.

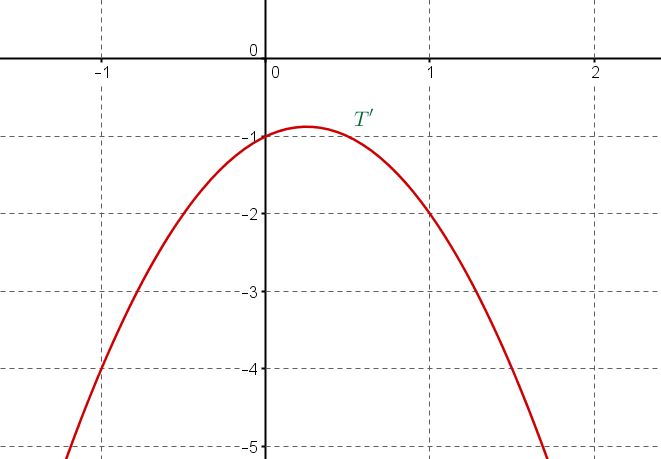
  2. On donne $f'(0)=1$.
    Déterminer l'équation réduite de la tangente $T'$ à la courbe au point d'abscisse 0 et la tracer dans le repère ci-dessus.

    Aide

    Il faut calculer $f(0)$

    Solution

    $f(0)=-2\times (0)^2+0-1=-1$
    On a donc:
    $y=f~'(0)(x-0)+f(0)$
    $\phantom{y}=1(x-0)-1$
    $\phantom{y}=x-1$

    $T'$ passe par le point $B(0;-1)$ et a pour coefficient directeur $1$.

devoir nº 793


Vous pouvez retourner sur le devoir après avoir vu cet exercice

Devoir tangentes et nombre dérivé

- lecture graphique du nombre dérivé
- équation d'une tangente
taux d'accroissement

infos cours

| 30mn

retour sur le devoir