1. Home
  2. chapitre 2 Dérivation
  3. exercice corrigé nº762
PDF reservé aux abonnés
La courbe $C_f$ ci-dessous représente la fonction $f$ définie et dérivable sur $[-4 ;5] $ et on note $f '$ la fonction dérivée de $f$ sur $[-4 ;5]$.

Les droites $(d)$, $(d')$ représentent les tangentes à la courbe $C_f$ respectivement aux points A et B d'abscisses $1$ et $0$
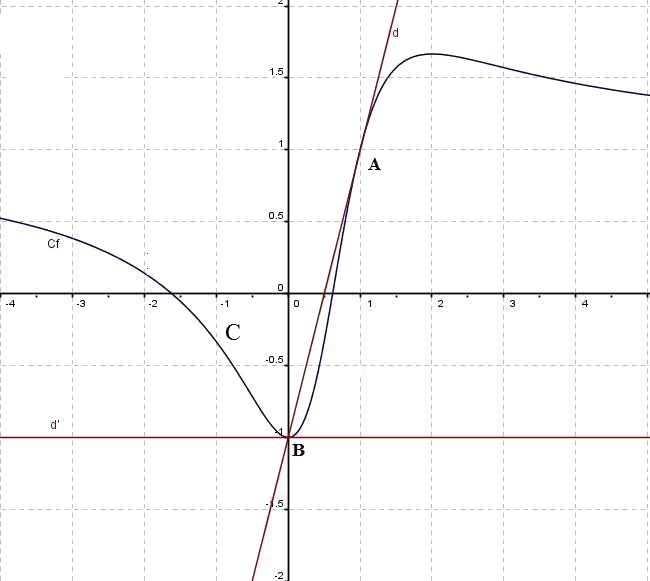
  1. Déterminer $f(1)$ en utilisant le graphique :

    Solution

    Le point A de coordonnées $(1;1)$ appartient à la courbe donc $f(1)=1$
  2. En utilisant le graphique, déterminer $f'(0)$ et $f'(1)$ en justifiant soigneusement les réponses.

    Rappel de cours

    Équation de la tangente au point d'abscisse $a$

    $f$ est une fonction définie et dérivable en $x=a$.
    La tangente à $C_f$ en $a$ a pour coefficient directeur $f'(a)$
    et pour équation réduite $ y=f'(a)(x-a)+f(a)$}

    Aide

    Graphiquement, il faut déterminer le coefficient directeur de la droite $(d')$.
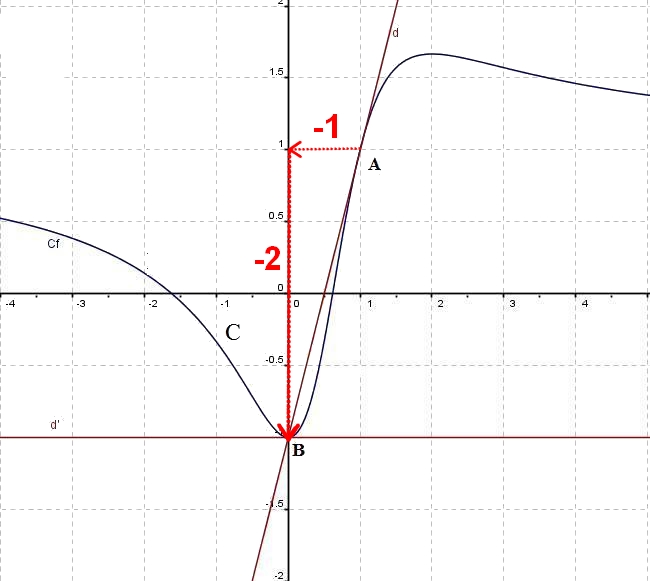
    Déterminer les coordonnées de deux points de la droite $(d')$ sur le graphique puis calculer le coefficient directeur de la droite $$$(d')$

    Solution

    $f'(0)$ est le coefficient directeur de la tangente $(d')$ à $C_f$ au points d'abscisse $0$ (point B)
    $(d)$ est parallèle à l'axe des abscisses donc a pour coefficient directeur 0 donc $f'(0)=0$
    $f'(1)$ est le coefficient directeur de la tangente $(d)$ à $C_f$ au points d'abscisse $1$ (point A) et passe par le point B
    donc $f'(1)=\dfrac{y_B-y_A}{x_B-x_A}=\dfrac{-1-1}{0-1}=\dfrac{-2}{-1}=2$

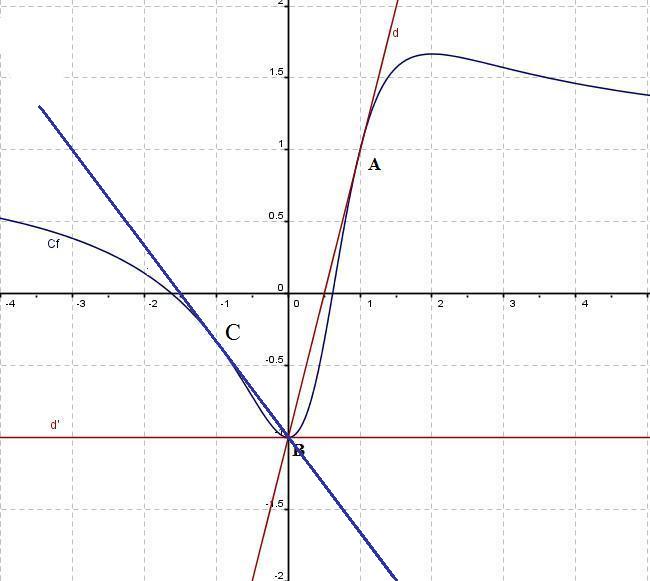
  3. Le point C est le point de la courbe de coordonnées $(-1;\dfrac{-1}{3})$ et on a $f'(-1)=\dfrac{-2}{3}$.
    Déterminer alors une équation de la tangente $T_{C}$ à la courbe $C_{f}$ au point C d'abscisse $-1$ puis la tracer.

    Aide

    $T_{C}$ a pour coefficient directeur $f'(-1)$
    L'équation réduite d'une droite est de la forme $y=ax+b$ avec $a$ coefficient directeur et $b$ ordonnée à l'origine.
    Pour déterminer $b$, on peut remplacer $x$ et $y$ par les coordonnées d'un point de la droite.
    Une autre méthode consiste à utiliser directement l'équation de la tangente en un point donnée en cours.

    Solution

    Méthode 1 (sans utiliser l'équation donnée en cours)
    $f'(-1)$ est le coefficient directeur de $T_C$ et $T_C$ passe par le point C.
    On a donc $T_C$: $y=\dfrac{-2}{3}x+b$
    et
    $A\in T_C$
    $\Longleftrightarrow y_C=\dfrac{-2}{3}x_C+b$
    $\Longleftrightarrow \dfrac{-1}{3}=\dfrac{-2}{3}\times (-1)+b$
    $\Longleftrightarrow b=-1$

    Avec la propriété du cours, on a aussi:
    $T_C$: $y=f'(a)(x-a)+f(a)$ avec ici $a=-1$
    $f'(a)=f'(-1)=\dfrac{-2}{3}$ et $f(a)=f(-1)=\dfrac{-1}{3})$
    Autre méthode (semblable à la démonstration du cours):
    $\overrightarrow{AM}(x+1;y+\dfrac{1}{3})$ et le vecteur $\overrightarrow{u}(1; f'(-1))$ colinéaires pour trouver une équation de $T_C$
    Pour tracer cette tangente, il faut utiliser le point C et déterminer les coordonnées d'un second point de la droite en prenant $x=3$ par exemple.
    On peut aussi utiliser le point C et le coefficient directeur $\dfrac{-2}{3}$. Un déplacement de 3 unités selon l'axe des ordonnées quand on effectue un déplacement de $-2$ selon l'axe des abscisses.

devoir nº 793


Vous pouvez retourner sur le devoir après avoir vu cet exercice

Devoir tangentes et nombre dérivé

- lecture graphique du nombre dérivé
- équation d'une tangente
taux d'accroissement

infos cours

| 30mn

retour sur le devoir