- Résoudre $\dfrac{5}{x-6}\leq 3x-2$
Signe de $ax^2+bx+c$
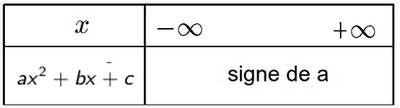
- Cas $\Delta>0$ (deux racines $x_1$ et $x_2$

- Cas $\Delta=0$ (une racine $x_1$)
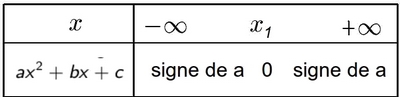
- Cas $\Delta<0$ (aucune racine)
 Il faut utiliser un tableau de signes avec un quotient
Il faut utiliser un tableau de signes avec un quotient
Pour obtenir ce quotient, il faut avoir 0 dans le membre de droite et réduire au même dénominateur dans le membre de gaucheIl faut $x-6\neq 0$ soit $x\neq 6$
On résout donc cette inéquation sur $D=\mathbb{R}\setminus \lbrace 6 \rbrace$
$\dfrac{5}{x-6}\leq 3x-2 \Longleftrightarrow \dfrac{5}{x-6}-(3x-2)\leq 0$
$\phantom{\dfrac{5}{x-6}\leq 3x-2} \Longleftrightarrow \dfrac{5}{x-6}-\dfrac{(3x-2)(x-6)}{x-6}\leq 0$
$\phantom{\dfrac{5}{x-6}\leq 3x-2} \Longleftrightarrow \dfrac{5-(3x-2)(x-6)}{x-6}\leq 0$
$\phantom{\dfrac{5}{x-6}\leq 3x-2} \Longleftrightarrow \dfrac{5-(3x^2-18x-2x+12)}{x-6}\leq 0$
$\phantom{\dfrac{5}{x-6}\leq 3x-2} \Longleftrightarrow \dfrac{5-3x^2+18x+2x-12}{x-6}\leq 0$
$\phantom{\dfrac{5}{x-6}\leq 3x-2} \Longleftrightarrow \dfrac{-3x^2+20x-7}{x-6}\leq 0$
Racines de $-3x^2+20x-7$
$\Delta=b^2-4ac=20^2-4\times (-3)\times (-7)=316$
$\Delta>0$ donc il y a deux racines
$x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-20 + \sqrt{316} }{-6 }=\dfrac{-20+2\sqrt{79}}{-6}=\dfrac{-2(10+\sqrt{79})}{-2\times 3}=\dfrac{10-\sqrt{79}}{3}$
et $x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-20- \sqrt{316} }{-6 }=\dfrac{10+\sqrt{79}}{3}$
On a $x_1\approx 0,4$ et $x_2 \approx 6,3$
Penser à contrôler les racines du numérateur avec le MENU équation de la calculatrice
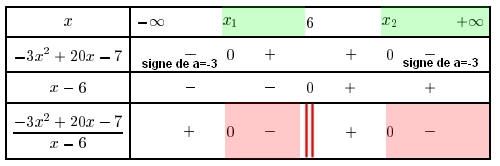
Le quotient doit être positif (zone rouge) pour $x$ appartenant à la zone verte ( valeur interdite!)
Avec une équation, on peut écrire $\dfrac{5}{x-6}= 3x-2=5=(3x-2)(x-6)$
mais on ne peut multiplier par $x-6$ avec une inéquation car selon le signe de $x-6$, l'inégalité change ou pas de sens et on ne connaît pas le signe de $x-6$ - Résoudre $\dfrac{x-1}{x-3}\geq x+2$
Il faut utiliser la même méthode que pour la question 1Il faut $x-3\neq 0$ soit $x\neq 3$
On résout donc cette inéquation sur $D=\mathbb{R}\setminus \lbrace 3 \rbrace$
$\dfrac{x-1}{x-3}\geq x+2 \Longleftrightarrow \dfrac{x-1}{x-3}-( x+2)\geq 0$
$\phantom{\dfrac{x-1}{x-3}\geq x+2} \Longleftrightarrow \dfrac{x-1}{x-3}-\dfrac{( x+2)(x-3)}{x-3}\geq 0$
$\phantom{\dfrac{x-1}{x-3}\geq x+2} \Longleftrightarrow \dfrac{x-1-( x+2)(x-3)}{x-3}\geq 0$
$\phantom{\dfrac{x-1}{x-3}\geq x+2} \Longleftrightarrow \dfrac{x-1-(x^2+2x-3x-6)}{x-3}\geq 0$
$\phantom{\dfrac{x-1}{x-3}\geq x+2} \Longleftrightarrow \dfrac{x-1-x^2-2x+3x+6)}{x-3}\geq 0$
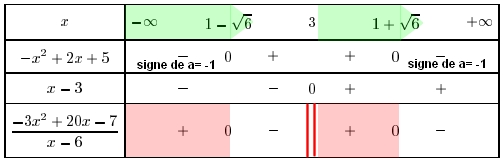
$\phantom{\dfrac{x-1}{x-3}\geq x+2} \Longleftrightarrow \dfrac{-x^2+2x+5}{x-3}\geq 0$
Racines de $-x^2+2x+5$
$\Delta=b^2-4ac=2^2-4\times (-1)\times 5=4+20=24$
$\Delta>0$ donc il y a deux racines
$x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-2 + \sqrt{28} }{-2 }=\dfrac{-2+2\sqrt{6}}{-2}=\dfrac{-2(1-\sqrt{6})}{-2\times 1}=1-\sqrt{6}$
et $x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-2- \sqrt{24} }{-2 }=1+\sqrt{6}$
On a $x_1\approx -1,4$ et $x_2 \approx 3,4$
Penser à contrôler les racines du numérateur avec le MENU équation de la calculatrice
Attention les fonctions ci-dessous sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Cours nº 592
Vous pouvez retourner sur le cours après avoir vu cette vidéo.
Signe de $ax^2+bx+c$
- tableau de signe de $ax^2+bx+c$ en fonction du nombre de racines
- exemples d'inéquations du second degré
infos cours
| 10-15mn
série 8 : Signe et inéquations du second degré
Fiche méthode
Si cet exercice vous pose problème, nous vous conseillons de consulter la fiche méthhode.
Inéquations commentées pas à pas
Exemples de résolution d'inéquations en utilisant le signe du polynôme du second degré
infos: | 8-12mn |
exercices semblables
Si vous souhaitez vous emtraîner un peu plus, nous vous conseillons ces exercices.
Signe d'un produit ou d'un quotient
| 8-12mn |
Inéquations du second degré avec un produit ou quotient
| 10-12mn |
| 8-12mn |
Inéquations du second degré avec un produit ou quotient
| 10-12mn |