Exercice 1 (5 points)
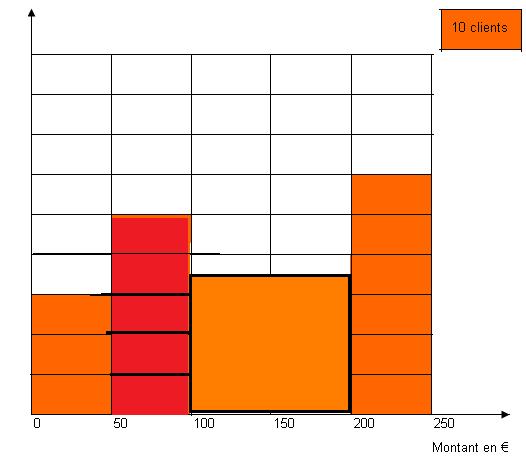
L'histogramme ci-dessous donne le nombre de clients d'un site Internet en fonction du montant de leurs achats.
- Déterminer le nombre de client ayant effectué un achat d'un montant compris entre 50 et 100 euros.
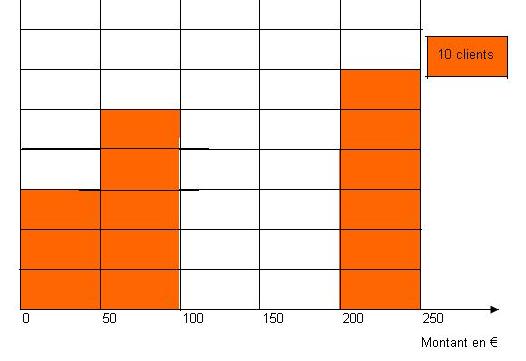
- 70 clients on effectué un achat d'un montant compris entre 100 et 200 euros, compléter le graphique avec le rectangle correspondant.
- Calculer la moyenne de cette série de donnée et en donner la signification.
Moyenne
On considère la série de $N$ données $x_i$ ($i$ entier naturel compris entre $1$ et $N$) les valeurs du caractère et $n_i$ les effectifs correspondants.
$N=n_1+n_2+$.... est l'effectif total.
La moyenne de la série statistique est $\overline{x}=\dfrac{n_1x_1+n_2x_2+\text{.....}+n_px_p}{N}$.} Dans le cas d'une série regroupée en classe, on utilise le centre des classes pour faire le calcul de la moyenne.Il faut utiliser le centre des intervalles et déterminer les effctifs correspondants en utilisant l'aire de chacun des rectangles.Pour un montant compris entre 0 et 50 euros (centre 25), il y a 30 clients.
Pour un montant compris entre 50 et 100 euros (centre 75), il y a 50 clients.
Pour un montant compris entre 100 et 200 euros (centre 150), il y a 70 clients.
Pour un montant compris entre 200 et 250 euros (centre 225), il y a 60 clients.
$m=\dfrac{30\times 25+50\times 75+70\times 150+60\times 225}{30+50+70+60}\simeq 135,71$
Exercice 2 (6 points)
- Lors d'une enquête, quatre enquêteurs ont interrogé des personnes pour connaître le nombre kilomètres qu'elles parcourent en train chaque année. Ils ont obtenu respectivement les résultats suivants :
Le premier enquêteur a interrogé 298 personnes et a obtenu une moyenne de 64 km parcourus chaque année. Le second enquêteur a interrogé 702 personnes et a obtenu une moyenne de 124 km parcourus chaque année. Le troisième enquêteur a interrogé 2000 personnes et a obtenu une moyenne de 42,19 km parcourus chaque année.
Quelle est la distance moyenne parcourue en train chaque année par les 3000 personnes interrogées par ces trois enquêteurs ?Moyenne
On considère la série de $N$ données $x_i$ ($i$ entier naturel compris entre $1$ et $N$) les valeurs du caractère et $n_i$ les effectifs correspondants.
$N=n_1+n_2+$.... est l'effectif total.
La moyenne de la série statistique est $\overline{x}=\dfrac{n_1x_1+n_2x_2+\text{.....}+n_px_p}{N}$.} Dans le cas d'une série regroupée en classe, on utilise le centre des classes pour faire le calcul de la moyenne.Il faut calculer la moyenne en tenant compte des effectifs pour chaque enquêteur.$m=\dfrac{298\times 64+702\times 124+2000\times 42,19}{298+702+2000}=63,5$
- Un quatrième enquêteur se souvient avoir obtenu une moyenne de 85,5 km parcourus chaque année pour les personnes qu'il a interrogées et la moyenne pour l'ensemble des personnes interrogées par les quatre enquêteurs était alors de 69 km parcourus chaque année. Combien de personnes a interrogé ce quatrième enquêteur ?
Il faut écrire une équation d'inconnue $x$ (nombre de personnes interrogées) pour que la moyenne soit de 85,5km$m=\dfrac{298\times 64+702\times 124+2000\times 42,19+x\times 85,5}{298+702+2000+x}=69 \Longleftrightarrow \dfrac{190500+85,5x}{3000+x}=69$
$\phantom{m=\dfrac{298\times 64+702\times 124+2000\times 42,19+x\times 85,5}{298+702+2000+x}=69} \Longleftrightarrow \dfrac{190500+85,5x}{3000+x}=69$
$\phantom{m=\dfrac{298\times 64+702\times 124+2000\times 42,19+x\times 85,5}{298+702+2000+x}=69} \Longleftrightarrow 190500+85,5x=(3000+x)69$
$\phantom{m=\dfrac{298\times 64+702\times 124+2000\times 42,19+x\times 85,5}{298+702+2000+x}=69}\Longleftrightarrow 190500+85,5x=207000+69x$
$\phantom{m=\dfrac{298\times 64+702\times 124+2000\times 42,19+x\times 85,5}{298+702+2000+x}=69}\Longleftrightarrow 85,5x-69x=207000-190500$
$\phantom{m=\dfrac{298\times 64+702\times 124+2000\times 42,19+x\times 85,5}{298+702+2000+x}=69}\Longleftrightarrow 16,5x=16500$
$\phantom{m=\dfrac{298\times 64+702\times 124+2000\times 42,19+x\times 85,5}{298+702+2000+x}=69}\Longleftrightarrow x=\dfrac{16500}{16,5}=1000$
Exercice 3 (9 points)
- On a demandé aux 35 élèves d'une classe de première, la première L1, le temps consacré à la lecture pendant une semaine.
Les résultats sont consignés dans le diagramme en boîte numéro 1.
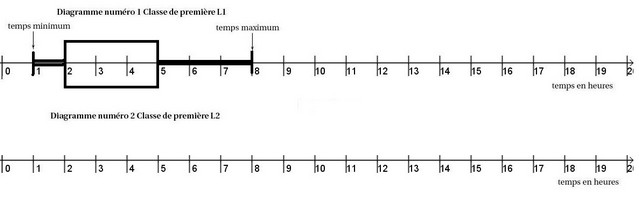
- Déterminer $Q_1$ et $Q_3$ premier et troisième quartile.
Diagramme en boîte
Sur un axe gradué, on doit placer le minimum, $Q_1$, médiane, $Q_3$ et la valeur maximale.
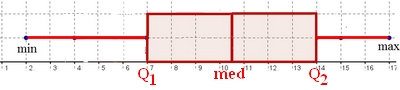
- Pour cette classe, le temps moyen de lecture est de 4 heures et le
temps médian de lecture est de 3 heures.
Compléter le diagramme en boîte numéro 1, en plaçant le temps moyen (le marquer par une croix ) et le temps médian.Diagramme en boîte
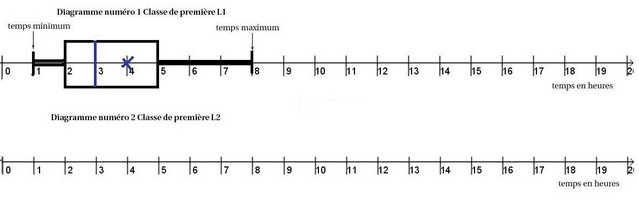
- Pourquoi peut-on affirmer qu'au moins 26 élèves de ce groupe lisent
5 heures par semaine ou moins ? Justifier la réponse.
Quartiles
Le premier quartile $Q_1$ est la plus petite valeur du caractère telle que au moins 25% (un quart) des valeurs soient inférieures ou égales à $Q_1$.
Le troisième quartile $Q_3$ est la plus petite valeur du caractère telle que au moins 75% (trois quarts) des valeurs soient inférieures ou égales à $Q_3$.
L'intervalle $[Q_1;Q_3]$ est l'intervalle interquartile et $Q_3-Q_1$ est l'écart interquartile.On peut utiliser le troisième quartile pour répondre.$Q_3=5$ signifie qu'au moins 75% des élèves lisent 5h ou moins.
$\dfrac{75}{100}\times 35=26,25$
- Déterminer $Q_1$ et $Q_3$ premier et troisième quartile.
- On pose à la classe de Première L2, composée de 25 élèves, la même
question. Les résultats individuels sont consignés dans le tableau
ci-dessous :
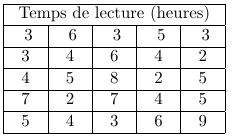
On considère la série statistique formée des 25 temps de lecture.- Ordonner les données en complétant le tableau ci-dessous:
 .
.
- Déterminer pour cette série statistique le minimum, le maximum,
la médiane et la moyenne.
Déterminer le premier quartile $Q_1$ et le troisième quartile $Q_3$.Médiane
La médiane $M$ est la valeur du caractère telle que a 50% (la moitié) des valeurs soient inférieures ou égales à $M$ et l'autre moitié supérieures ou égale à $M$.
Exemple 1: Si l'effectif total est pair (par exemple 14 valeurs) alors la médiane est entre la 7ième et la 8ième valeur(valeurs classées dans l'ordre croissant)
Exemple 2: Si l'effectif total est impair (par exemple 15 valeurs) alors la médiane correspond à la 8ième valeur(valeurs classées dans l'ordre croissant)Quartiles
Le premier quartile $Q_1$ est la plus petite valeur du caractère telle que au moins 25% (un quart) des valeurs soient inférieures ou égales à $Q_1$.
Le troisième quartile $Q_3$ est la plus petite valeur du caractère telle que au moins 75% (trois quarts) des valeurs soient inférieures ou égales à $Q_3$.
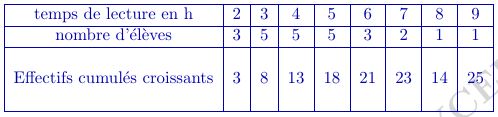
L'intervalle $[Q_1;Q_3]$ est l'intervalle interquartile et $Q_3-Q_1$ est l'écart interquartile.Le minimum est 2h, le maximum est 9h.
Il y a 25 élèves (efefctif impair) donc la médiane est le temps de lecture du 13ième élève si on classe les données dans l'ordre croissant du temps de lecture soit $med=4$h
La moyenne est $\dfrac{2\times 3 +3\times 5 +4\times 5 +5\times 5 +6\times 3 +7\times 2 +8\times 1 +9\times 1}{25}=4,6$ h.
$\dfrac{25}{100}\times 25=6,25$
donc $Q_1$ correspond au temps de lecture du 7 ième élève soit $Q_1=3$
$\dfrac{75}{100}\times 25=18,75$
donc $Q_3$ correspond au temps de lecture du 19 ième élève soit $Q_3=6$ - Compléter le graphique avec le diagramme en boîte de cette seconde série de données.
.
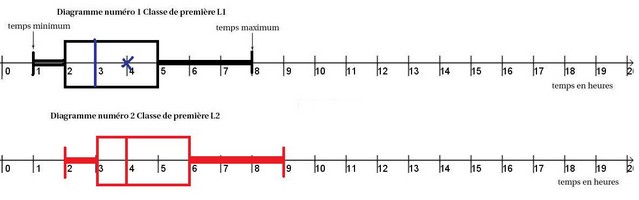
- Ordonner les données en complétant le tableau ci-dessous:
- Calculer le temps de lecture moyen pour l'ensemble des deux classes.
Fiche méthode
Si ce devoir vous pose problème, nous vous conseillons de consulter la fiche méthhode.
Médianes et quartiles avec une série discrète
- définitions
- méthode
- exemple
infos: | 10mn |
vidéos semblables
Pour compléter ce devoir, nous vous conseillons les vidéos suivantes pour préparer ce devoir.
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.