Exercice 1 (7 points)
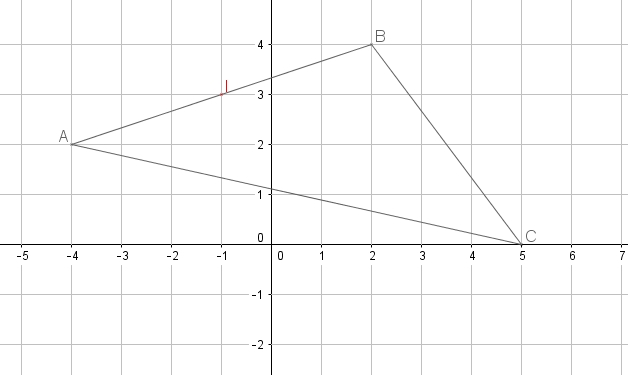
On donne le triangle $ABC$ avec $A(-4;2)$, $B(2;4)$ et $C(5;0)$ dans un repère orthonormé du plan.
- Placer les points $A$, $B$ et $C$ dans le repère.
- Calculer les coordonnées du milieu $I$ de $[AB]$ et tracer la droite $(d)$ d'équation $y=\dfrac{-x+5}{2}$.
Que représente la droite $(d)$ pour le triangle $ABC$? (justifier la réponse)Coordonnées du milieu d'un segment
Dans un repère du plan, si on a $A(x_A;y_A)$ et $B(x_B;y_B)$ alors le milieu $I$ de $[AB]$ a pour coordonnées $I\left(\dfrac{x_A+x_B}{2};\dfrac{y_A+y_B}{2}\right)$Il faut vérifier que $A$ et $I$ appartiennent à $(d)$$x_I=\dfrac{x_A+x_B}{2}=\dfrac{-4+2}{2}=-1$
et $y_I=\dfrac{y_A+y_B}{2}=\dfrac{0+4}{2}=2$
Tracé de $(d)$ d'équation $y=\dfrac{-x+5}{2}$
Si $x=1$, on a $y=\dfrac{-1+5}{2}=2$
et si $x=3$ on a $y=\dfrac{3+5}{2}=4$
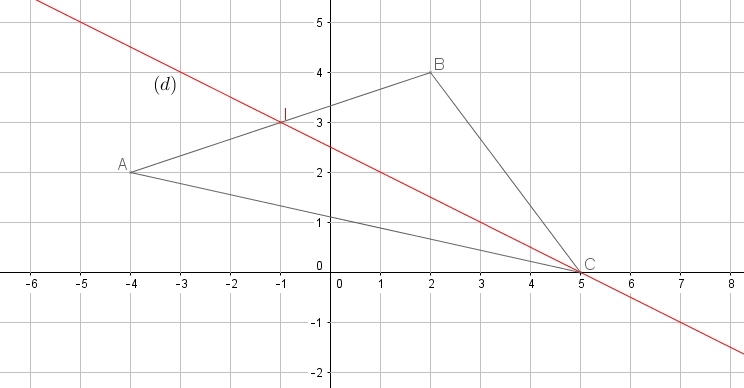
$\dfrac{-x_I+5}{2}=\dfrac{-(-1)+5}{2}=3=y_I$ donc $I\in (d)$
$\dfrac{-x_C+5}{2}=\dfrac{-5+5}{2}=0=y_C$ donc $C\in (d)$
donc $(d)$ passe par le sommet $C$ et le milieu de $[AB]$
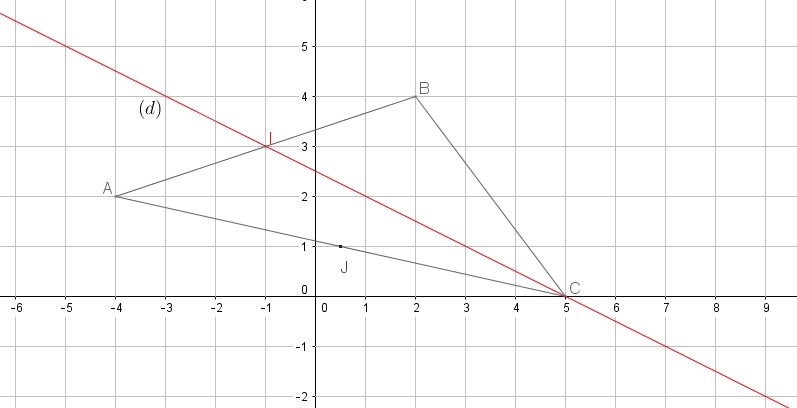
- Déterminer l'équation réduite de la médiane $(d_1)$ issue de $B$ dans $ABC$.
Déterminer l'équation réduite de $(AB)$
Dans un repère du plan, si $A(x_A;y_A)$ et $B(x_B;y_B)$ avec $x_A\neq x_B$, pour déterminer l'équation réduite de $(AB)$:
- Calcul du coefficient directeur
$a=\dfrac{\Delta_y}{\Delta_x}=\dfrac{y_B-y_A}{x_B-x_A}$
- Calcul de $b$
Le point $A$ appartient à la droite $(AB)$ donc ses coordonnées vérifient $y_A=ax_A+b$ (équation d'inconnue $b$)Il faut déterminer l'équation réduite de $(BJ)$ avec $J$ milieu de $[AC]$Coordonnées du milieu $J$ de $[AC]$:
$x_J=\dfrac{x_A+x_C}{2}=\dfrac{-4+5}{2}=\dfrac{1}{2}$
et $y_J=\dfrac{y_A+y_C}{2}=\dfrac{2+0}{2}=1$
donc $J\left(\dfrac{1}{2};1\right)$
Equation réduite de $(BJ)$ médiane issue de $B$ dans $ABC$:
$a=\dfrac{y_J-y_B}{x_J-x_B}=\dfrac{1-4}{\dfrac{1}{2}-2}=\dfrac{-3}{\dfrac{-3}{2}}=-3\times \dfrac{2}{-3}=2$
L'équation réduite de $(BJ)$ est donc de la forme $y=2x+b$
$B\in (BJ)$ donc $y_B=2x_B+b$
soit $4=2\times 2+b$ donc $b=0$.
La droite $(BJ)$ passe bien par l'origine du repère donc $b=0$ - Déterminer les coordonnées du point d'intersection $G$ des droites $(d)$ et $(d_1)$
Que représente $G$ pour $ABC$ ?il faut résoudre le système formé avec les deux équations de droitesL'équation réduite de $(d)$ est $y=\dfrac{-x+5}{2}$ et celle de $(d_1)$ est $y=2x$
Les coordonnées de $G$ doivent vérifier l'équation de $(d)$ et celle de $(d_1)$
donc il faut résoudre l'équation $\dfrac{-x+5}{2}=2x$.
$\dfrac{-x+5}{2}=2x$
$\Longleftrightarrow -x+5=4x$
$\Longleftrightarrow 5=5x$
$\Longleftrightarrow x=1$
donc $x_G=1$ et $y_G=2\times x_G=2$
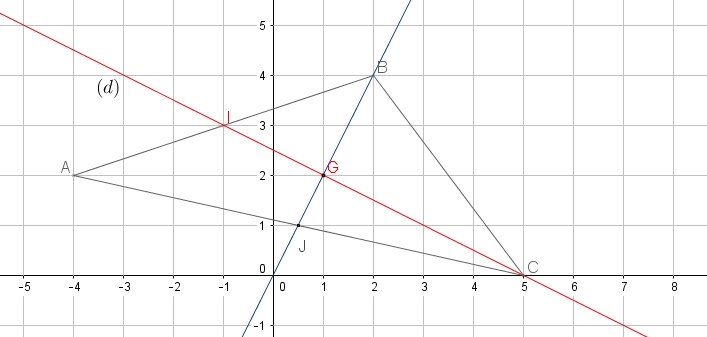
Contrôle du calcul: $\dfrac{-x_G+5}{2}=\dfrac{-1+5}{2}=2=y_G$ donc $G$ appartient bien à $(d_1)$
Exercice 2 (13 points)
Le plan est muni d'un repère orthogonal donné ci-dessous.
\includegraphics[scale=0.8]{fig1}
- Déterminer l'équation réduite de la droite $(d_1)$ puis celle de $(d_2)$ en utilisant le graphique.
Déterminer l'équation réduite de $(AB)$
Dans un repère du plan, si $A(x_A;y_A)$ et $B(x_B;y_B)$ avec $x_A\neq x_B$, pour déterminer l'équation réduite de $(AB)$:
- Calcul du coefficient directeur
$a=\dfrac{\Delta_y}{\Delta_x}=\dfrac{y_B-y_A}{x_B-x_A}$
- Calcul de $b$
Le point $A$ appartient à la droite $(AB)$ donc ses coordonnées vérifient $y_A=ax_A+b$ (équation d'inconnue $b$)Pour la droite $(d_1)$, on peut lier le coefficient directeur et l'ordonnée à l'origine directement sur le graphique
Pour la droite $(d_2)$, il faut calculer l'ordonnée à l'origine en utilisant un point de $(d_2)$Pour la droite $(d_1)$:
Coefficient directeur: $a_1=\dfrac{\Delta_y}{\Delta_x}=\dfrac{+3}{+3}=1$
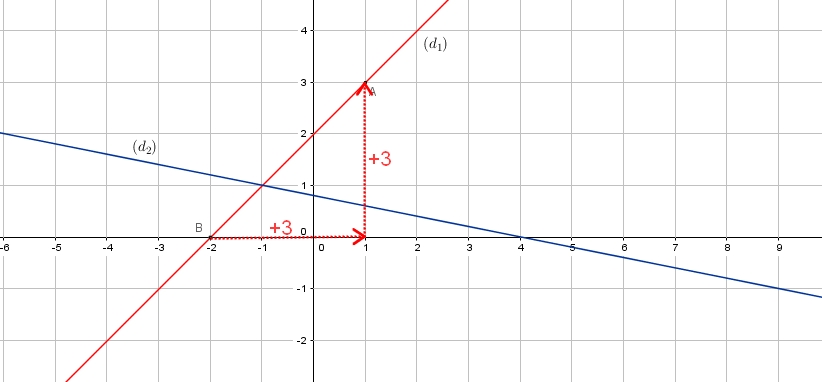
Ordonnée à l'origine:
La droite $(d_1)$ coupe l'axe des ordonnées en $y=2$ donc $b_1=2$
Pour la droite $(d_2)$:
Coefficient directeur: $a_2=\dfrac{\Delta_y}{\Delta_x}=\dfrac{+1}{-5}=\dfrac{-1}{5}$
Ordonnée à l'origine:
La droite $(d_2)$ a donc une équation réduite de la forme $y=\dfrac{-1}{5}x+b_2$
Le point $C(9;-1)$ appartient à la droite $(d_2)$ donc $y_C=\dfrac{-1}{5}x_C+b_2$
$-1=\dfrac{-1}{5}\times 9+b_2 \Longleftrightarrow -1=\dfrac{-9}{5}+b_2$
$\phantom{-1=\dfrac{-1}{5}\times 9+b_2} \Longleftrightarrow -1+\dfrac{9}{5}=b_2$
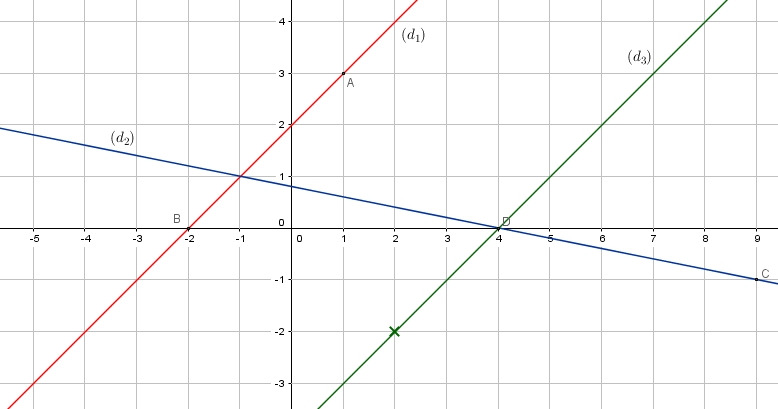
$\phantom{-1=\dfrac{-1}{5}\times 9+b_2} \Longleftrightarrow \dfrac{4}{5}=b_2$ - Tracer, sur le graphique, la droite $d_3$ d'équation $y=x-4$ et justifier que $(d_3)$ et $(d_2)$ sont parallèles.
Tracer une droite
Pour tracer une droite donnée par une équation cartésienne, on peut:
1. choisir deux valeurs de $x$ et calculer l'ordonnée correspondante avec l'équation de $(d)$ et placer les deux points obtenus
2. utiliser un vecteur directeur de $(d)$ et calculer l'ordonnée d'un point de $(d)$ en choisissant une valeur de $x$On peut utiliser l'ordonnée à l'origine et le coefficient directeur ou bien déterminer les coordonnées de deux points de la droite $(d_3)$Si $x=0$ alors on a $y=-4$ (ordonnée à l'origine)
et si $x=2$ alors $y=2-4=-2$
le coefficient directeur de $(d_3)$ est $a_3=1$ et celui de $(d_1)$ est $a_1=1$
donc $a_1=a_3$
- Déterminer les coordonnées du point $D$, point d'intersection de $(d_3)$ et de l'axe des abscisses.
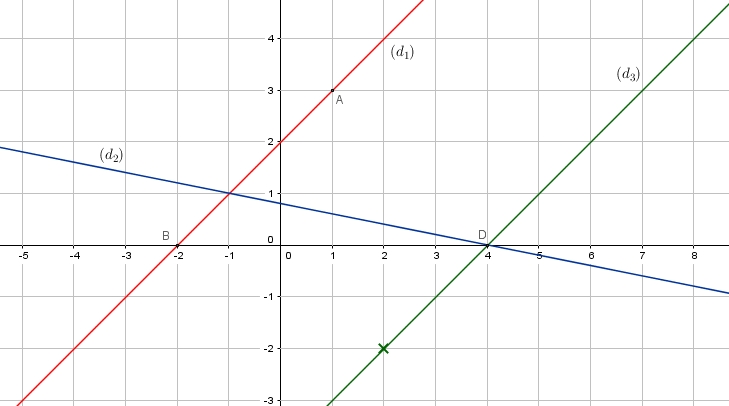
$D$ appartient-il à $(d_2)$? - Justifier que $(d_1)$ et $(d_2)$ sont sécantes et calculer les coordonnées de leur point d'intersection que l'on nommera $I$.
Il faut que les coordonnées de $I$ vérifient l'équation de $(d_1)$ et aussi de $(d_2)$.L'équation réduite de $(d_1)$ est $y=x+2$ et celle de $(d_2)$ est $y=\dfrac{-1}{5}x+\dfrac{4}{5}$.
Le coefficient directeur de $(d_1)$ est $a_1=1$ et celui de $(d_2)$ est $a_2=\dfrac{-1}{5}$
donc $a_1\neq a_2$
Les coordonnées de $I$ doivent vérifier l'équation de $(d_1)$ et celle de $(d_2)$
donc on doit avoir $x+2=\dfrac{-1}{5}x+\dfrac{4}{5}$.
$\phantom{\Longleftrightarrow}x+2=\dfrac{-1}{5}x+\dfrac{4}{5}$
$\Longleftrightarrow 5x+10=-x+4$ (on multiplie tous les termes par 5 pour se "débarasser" des fractions)
$\Longleftrightarrow 6x=-6$
$\Longleftrightarrow x=-1$
On a donc $x_I=-1$ et $y_I=x_I+2=-1+2=1$
- On donne $A(1;3)$, vérifier que $A$ appartient à $(d_1)$ et déterminer l'équation réduite de $(d_4)$ parallèle à $(d_2)$ et passant par $A$ et la tracer.
$(d_4)$ et $(d_2)$ on le même coefficient directeur et les coordonnées de $A$ doivent vérifier l'équation de $(d_4)$$(d_1)$ a pour équation réduite $y=x+2$
$x_A+2=1+2=3=y_A$
$(d_2)$ a pour coefficient directeur $a_2=\dfrac{-1}{5}$
donc $(d_4)$ parallèle à $(d_2)$ a pour coefficient directeur $a_2=\dfrac{-1}{5}$.
L'équation réduite de $(d_4)$ est de la forme $y=\dfrac{-1}{5}x+b_4$
$A(1;3)$ appartient à $(d_4)$ donc $y_A=\dfrac{-1}{5}x_A+b_4$
$3=\dfrac{-1}{5}\times 1+b_4$
$ \Longleftrightarrow 3+\dfrac{1}{5}=b_4$
$\Longleftrightarrow b_4=\dfrac{16}{5}$
Penser à contrôler que $(d_4)$ coupe l'axe des ordonnées en $y=b_4=\dfrac{16}{5}=3,2$
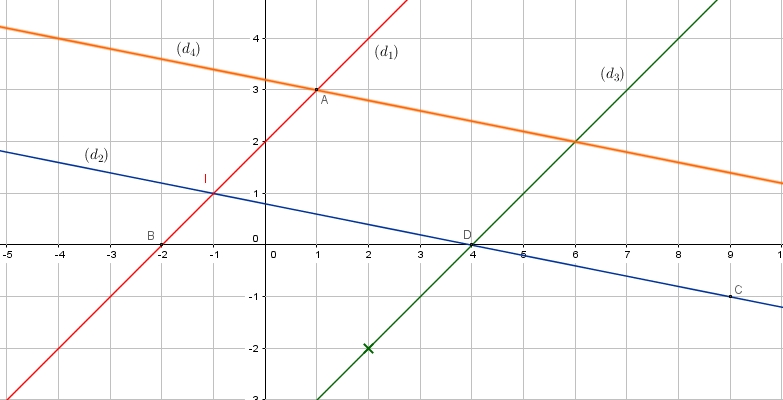
- Déterminer les coordonnées du point $J$, intersection des droites $(d_3)$ et $(d_4)$.
L'équation réduite de $(d_3)$ est $y=x-4$ et celle de $(d_4)$ est $y=\dfrac{-1}{5}x+\dfrac{16}{5}$
Les coordonnées de $J$ doivent vérifier l'équation de $(d_3)$ et celle de $(d_4)$
donc il faut résoudre l'équation $x-4=\dfrac{-1}{5}x+\dfrac{16}{5}$.
$x-4=\dfrac{-1}{5}x+\dfrac{16}{5}$
$\Longleftrightarrow 5x-20=-x+16$ (on multiplie tous les termes par 5 pour se "débarasser" des fractions)
$\Longleftrightarrow 6x=36$
$\Longleftrightarrow x=6$
donc $x_J=6$ et $y_J=x_J-4=6-4=2$
Contrôler les calculs en vérifiant que $J$ appartient bien à $(d_4)$.
$ \dfrac{-1}{5}x_J+\dfrac{16}{5}=\dfrac{-1}{5}\times 6+\dfrac{16}{5}=\dfrac{10}{5}=y_J$ donc $J\in (d_4)$.
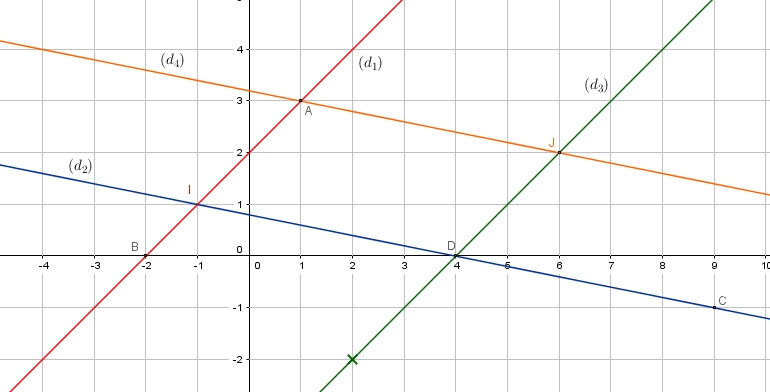
- Quelle est la nature du quadrilatère $AJDI$?
Fiche méthode
Si ce devoir vous pose problème, nous vous conseillons de consulter la fiche méthhode.
Équation réduite
- tracer une droite
- déterminer l'équation réduite
- déterminer l'équation réduite d'une parallèle
infos: | 20mn |
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.